Операція здобуття кореня n-ого степеня з комплексного числа

Нехай задане комплексне число .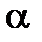

Означення Коренем n-ого (n≥2) степеня з комплексного числа 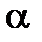називається комплексне число 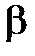таке, що

.

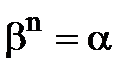Нехай число 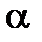задано в алгебраїчній формі 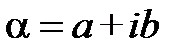. Шукатимемо 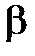також в алгебраїчній формі 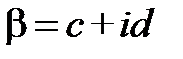. Розглянемо найпростіший випадок n=1. Тоді за попереднім означенням треба знайти дійсні числа с і d такі що

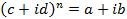
Тобто,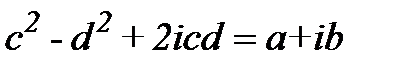

Порівнюючи дійсні та уявні частини, отримаємо дійсну нелінійну систему рівнянь.

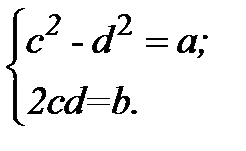
Більш складна система виникає, якщо таким шляхом вилучати корені степеня n≥3.

Розглянемо це питання для комплексного числа 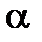заданого в тригонометричній формі .

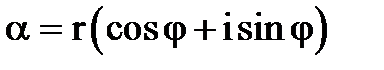Шукатимемо 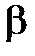також в тригонометричній формі .

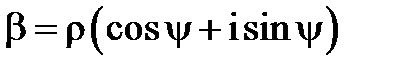За означенням, користуючись формулою Муавра, маємо

.

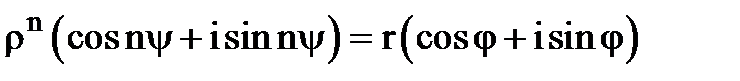З цієї рівності випливає

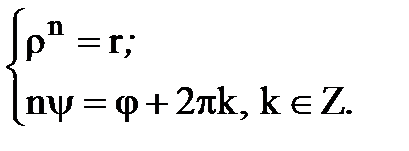
Звідси випливає 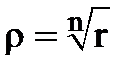(арифметичний корінь), .

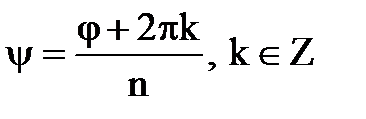Отже

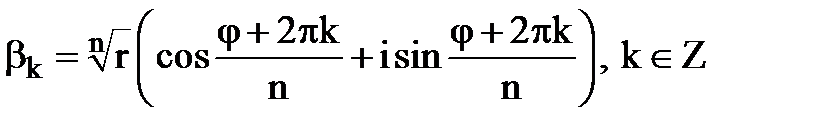
Насправді, щоб отримати всі корені достатньо змінювати 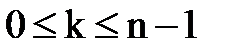. Нехай 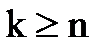. Доведемо, що збігатиметься з одним з коренів 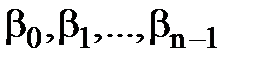. Поділимо к на n:

.

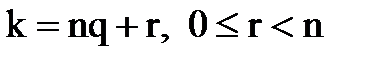Тоді

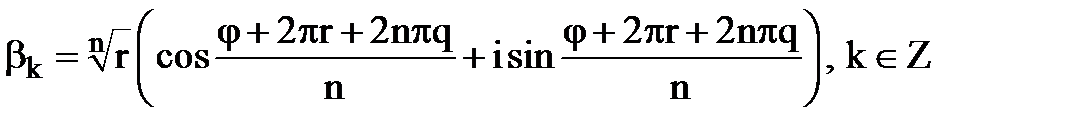
Скористаємося періодичністю тригонометричних функцій, тоді

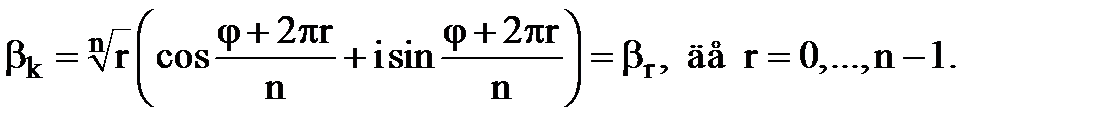
Отже, отримали формули

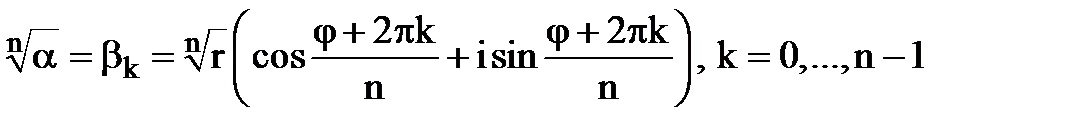
Зауваження В шкільному курсі символ 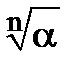вживався лише для арифметичних коренів. Тепер ми вживатимемо цей символ в більш широкому сенсі.