Доведення. Небхідність. Нехай матриця А має псевдообернену праву

Небхідність. Нехай матриця А має псевдообернену праву. Треба довести, що матриця А – рядковоневиродженна, тобто r A = s.

З того, що існує 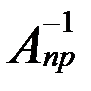, випливає А × 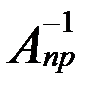= Е (s´s). З цього випливає, що rE=s. З теореми про ранг добутку матриць s = r E £ r A £ s. Тобто r A = s.

Достатність. Нехай матриця А – рядкововиродженна (r A = s). Треба довести, що існує 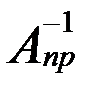. Для цього з’ясуємо, чи існує така матриця Х, що А × Х = Е.

Як відомо для можливості множення матриця Е має бути (s×s), а тоді Х має бути (n×s).

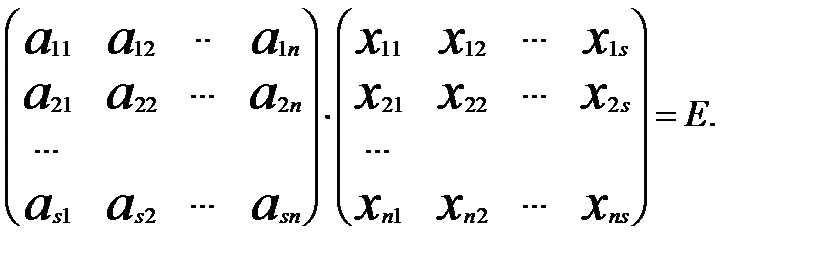
Отже матриця Х задовольняє умову:

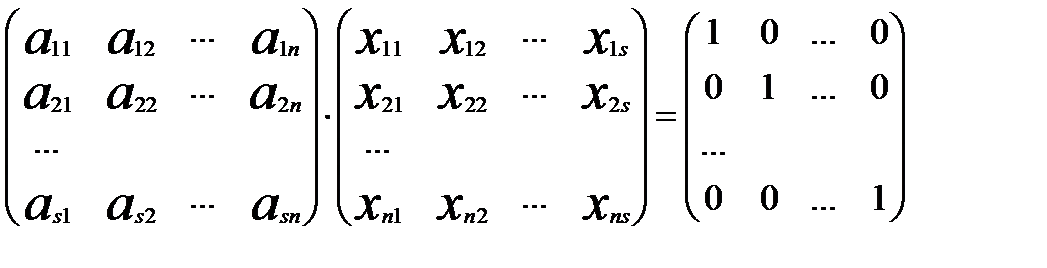. (4)

Безпосереднім множенням знайдемо елементи першого рядка добутку матриць

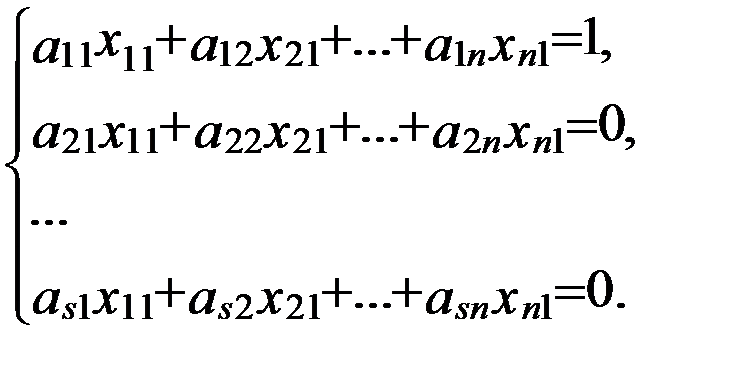(5)

Треба довести, що система (5) сумісна. Для цього треба довести, що виконуються умови теореми Кронекера-Капеллі:

.

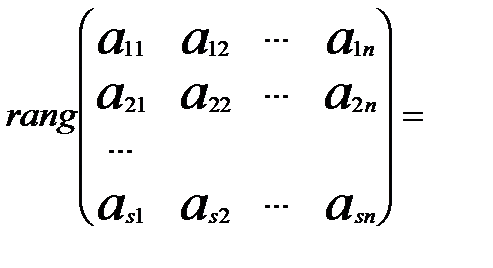
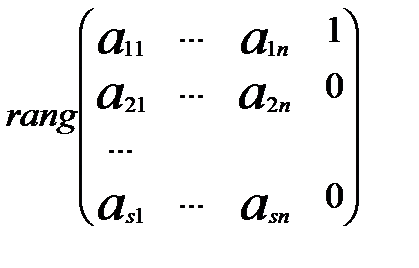За умовою теореми rA = s. Ранг r 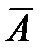також дорівнює s, тому що вона містить мінор s- го порядку, що не дорівнює нулю. Це мінор матриці А, а мінорів більш вищого порядку для 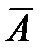утворити неможливо, тоді з теореми про ранг r 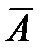= s.

Таким чином, виконується теорема Кронекера-Капеллі. Система (2) сумісна. Розв¢язавши її, знайдемо перший стовпчик шуканої матриці Х. Більш того, зауважемо, що система (2) має безліч розв¢язків. Оскільки r A = s < n, то виконуються умови критерія невизначеності. Так само отримаємо систему рівнянь, що містить другий стовпчик матриці Х:

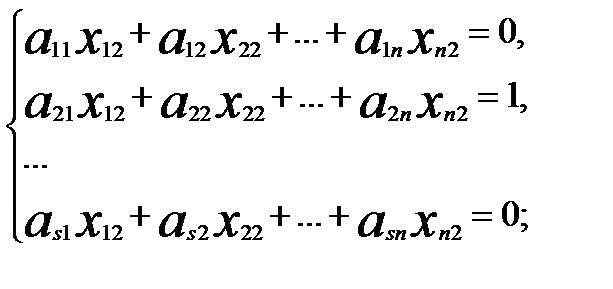
Так само доведемо, що система сумісна. Поступаючи аналогічним чином, отримаємо систему для останнього стовпця матриці Х.

Отже доведено, що існує псевдообернена права матриця Х для матриці А. Більш того, вона не єдина, їх безліч.