Закони множення

1. Множення матриць, взагалі кажучі, не комутативне. Для того, щоб в цьому переконатись,досить знайти дві матриці А і В, для яких А×В ¹ В×А.

А= 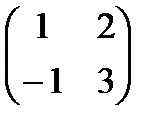, В= .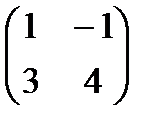

А×В = = ,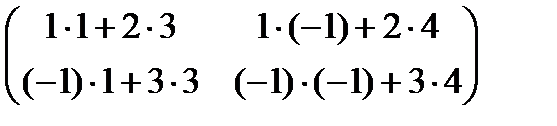

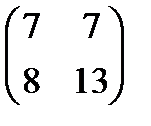В×А = = .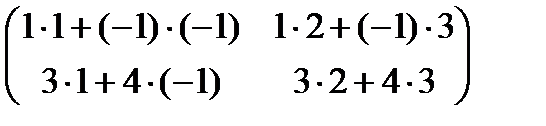

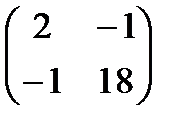З наведеного прикладу бачимо, що А×В ¹ В×А. При цьому ми виходили з такого означення рівних матриць.

Означення. Матриці А і В називаються рівними, якщо на одних і тих самих місцях знаходяться рівні елементи.

Теорема. Множення матриць підпорядковується асоціативному закону.

Тобто ми повинні довести, що для будь-яких матриць А, В і С має місце рівність

(А × В) × С = А × (В × С).

Нехай

А=(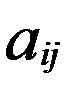), В=(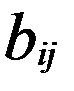). А × В = D = ()

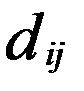(А × В) × С = C ×D = F (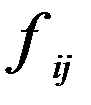), (В × С) = Р ()

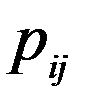А × (В × С) = А× Р = Т ().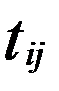

В цих позначеннях треба довести, що F = Т, тобто 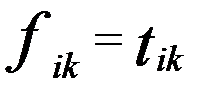( 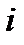= 1,2,…, )

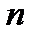Обчислимо

, (1)

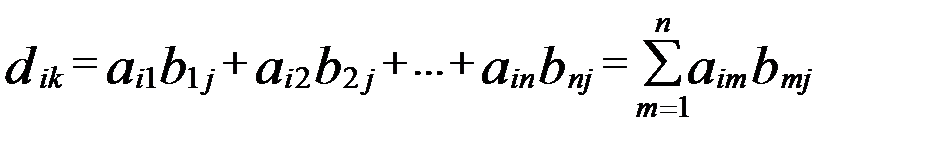, (2)

Підставимо (2) в (1), отримаємо

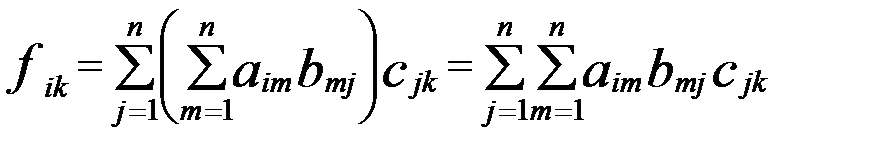(3)

Преходимо до обчислення .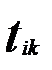

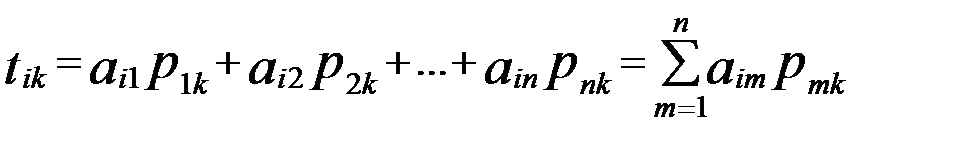(4)

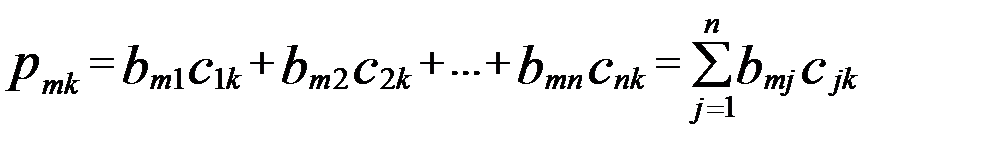(5)

Підставимо (5) в (4), отримаємо

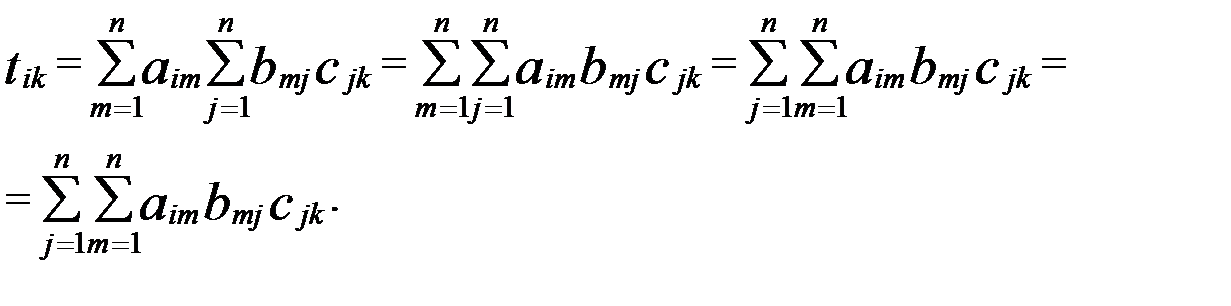(6)

Порівнюючи (3) і (6), приходимо до висавку, що , що й треба було довести.

Хоча множення матриць, взагалі кажучі, некомутативне, існує матриця, яка комутує з будь-якою матрицею А, і більш того, в добутку з даною матрицею не змінює цю матрицю А. Це так звана одинична матриця:

Е = .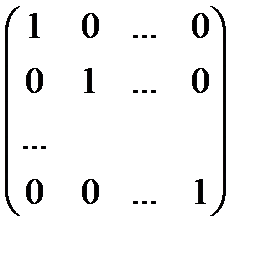

Ця матриця має такі властивості:

1) А × Е = А, " А

2) Е × А = А, " А,

а звідси випливає, що А × Е = Е × А.

Доведемо другу властивість.

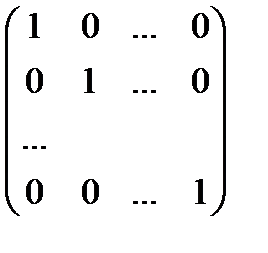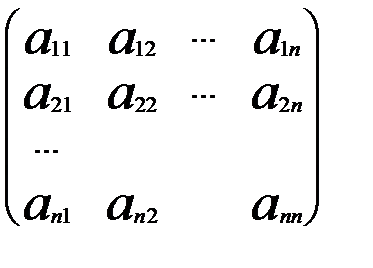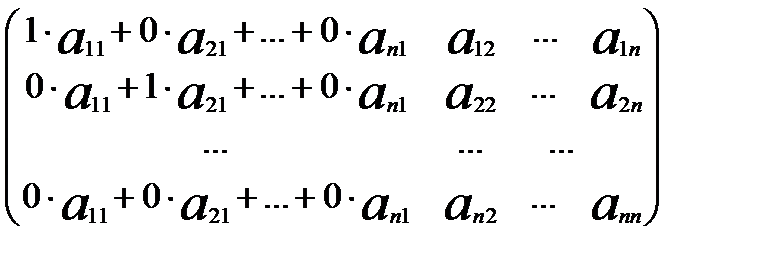Е × А = × =

= = А.

Так само доводиться перша властивість, тобто безпосереднім множенням.

Теорема. .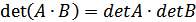

Доведеня. Нехай задано матриці А і В, а С – добуток цих матриць. Треба довести, що

det C = det A ×det B.

Для доведення побудуємо визначник d порядку 2n:

d = .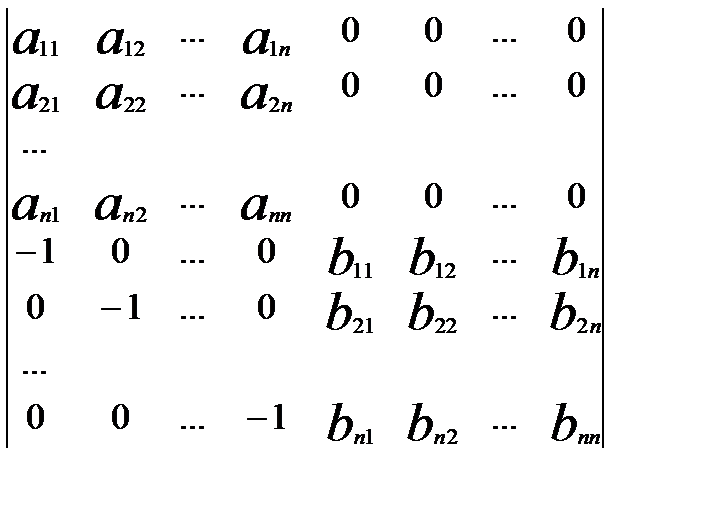

Застосуємо до перших n рядків цього визначника теорему Лапласа

d = det A ×det B (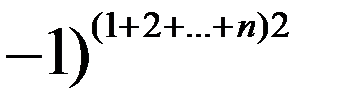, тобто

d = det A ×det B (1)

Перетворимо визначник d за допомогою восьмої властивості визначників. До (n+1) стовпчика додамо перший стовпець помножений на 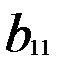, другий – на 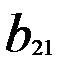, n-ий – на .

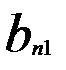Аналогічно зробимо з (n+2)-им стовпцем, (2n)-им стовпцем. В правому нижньому куті отримаємо нульовий блок порядку n. А правий верхній кут, тоді перетворюється в елементи матриці С.

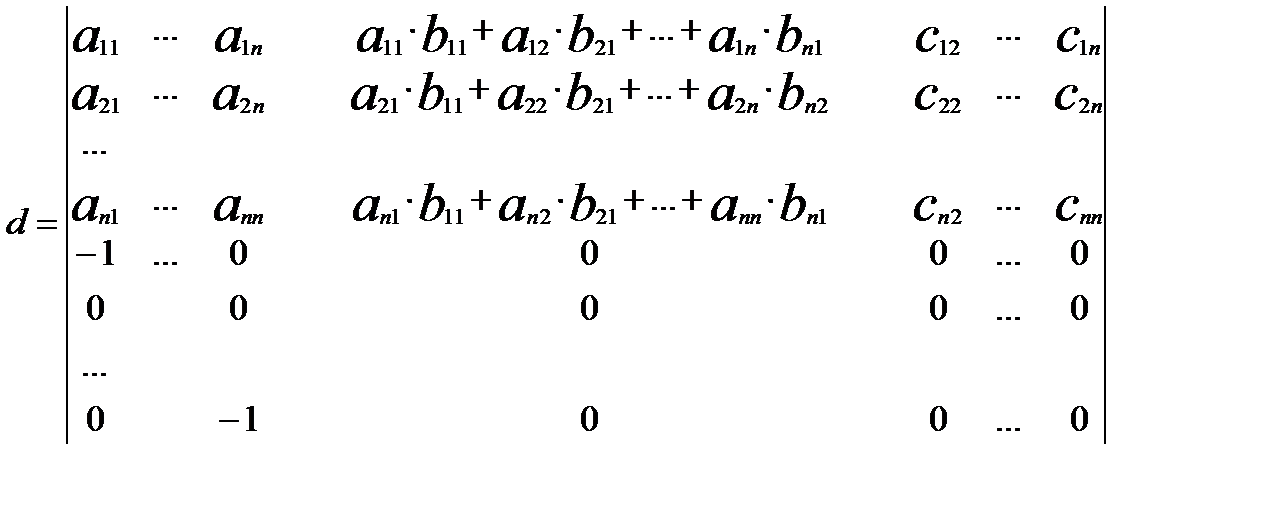
Застосуємо до цього визначника теорему Лапласа.

d = det C .

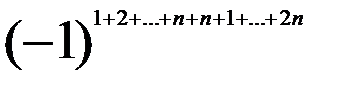Користуючись формулою суми 2n членів арифметичної прогресії, маємо

d = det C 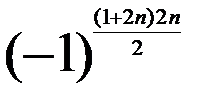, det C = det A × det B.

Вправа. Довести самостійно єдиність одиничної матриці (скористатись методикою доведення єдиності нульового вектора будь-якого лінійного простору).