Операції додавання і множення на число

Означення. Сумою матриць А і В, А=(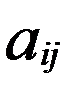), В=(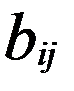), називається матриця D, елементи якої обчислюються за законом

D = ( + ).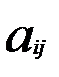

Означення. Добутком матриці А на число k, називається матриця F, елементи якої обчислюються за законом

F = (k ).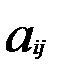

Введені операції мають такі властивості:

1) А + В = В + А;

2) (А + В)+С = А+(В + С);

3) $ Q: А + Q = А + Q + А;

Q = .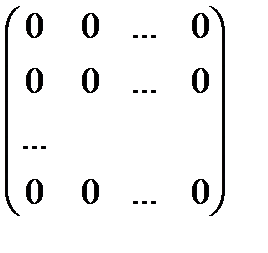

4) " А $ (-А): А + (-А) = (-А) + А = 0.

Вона і снує, тому що є (-А) = (- ).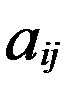

5) А = А;

6) k (l A) = (k l) A;

7) k (A + B) = kA + kB;

8) (k + l) A = kA + lA:

Перевірити самостійно.

Таким чином, множина всіх матриць є векторним простором, більш того, арифметичним, вимірності .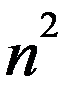

Розглянемо хоча б один базіс цього простору. Це так звані матриці .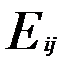

= .

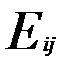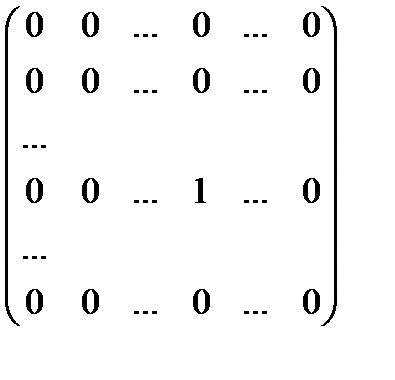Таких матриць існує n².

, , …, ,

, , …,

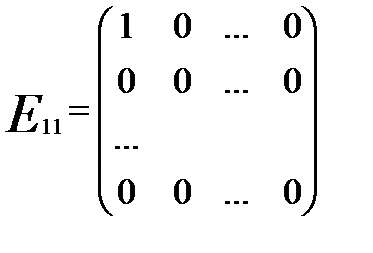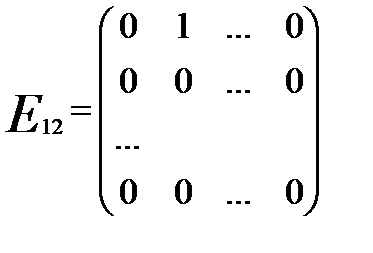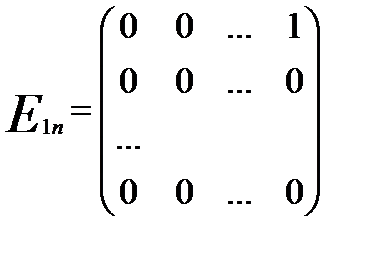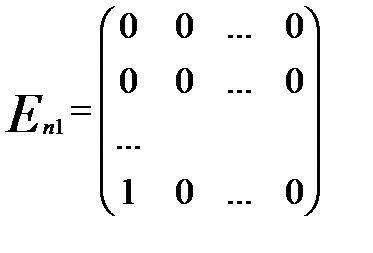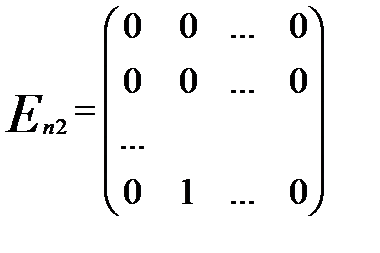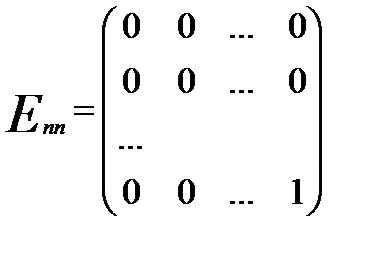
Доведемо, що це базис. Доведемо, що це лінійно незалежні матриці. Для цього з’ясуємо, при яких k_ij виконується рівність

(*)

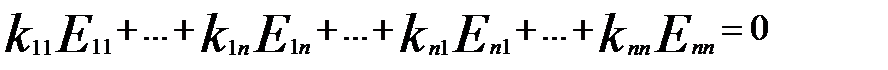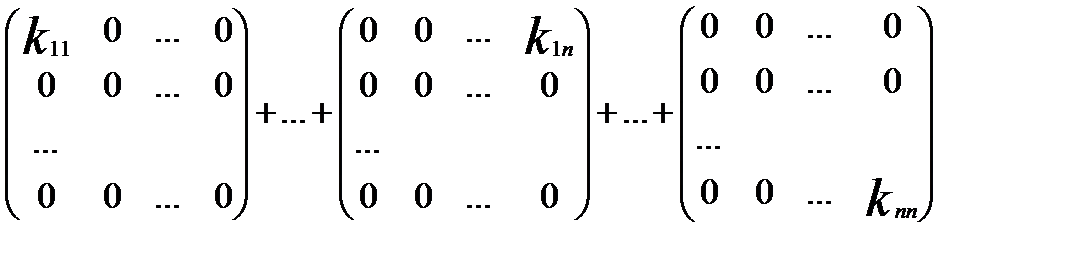= 0.

, .

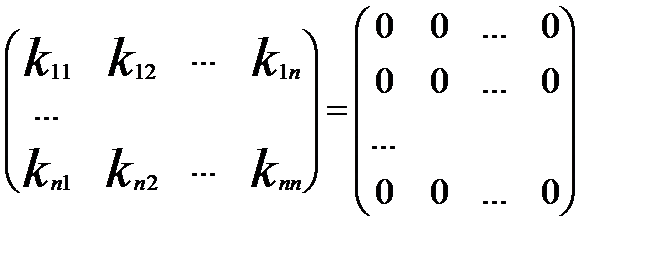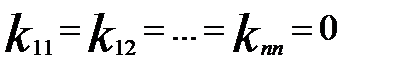Отже рівність (*) виконується лише в нульовому випадку усіх k_ij, тому матриці лінійно залежні.

З того, що вимерність простору матриць дорівнює 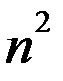, випливає, що матриці 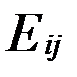утворюють базіс. Тоді будь-яка матриця А повинна бути лінійною комбінацією матриць 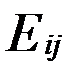. Знайдемо цю лінійну комбнацію.

Розглянемо довільну матрицю А. Доведемо, що

А = .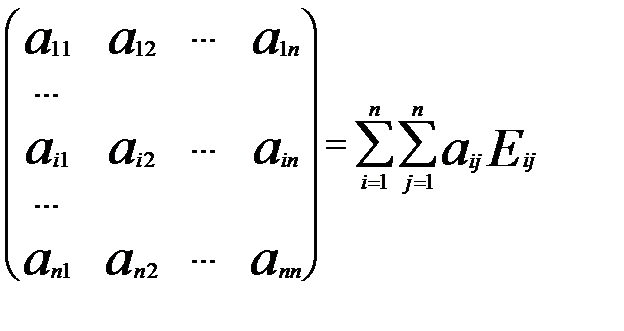

Введемо в розгляд допоміжну матрицю:

.

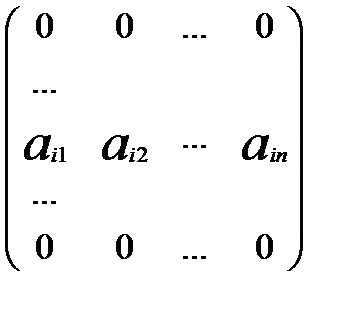Доведемо, що цю матрицю можна подати у вигляді .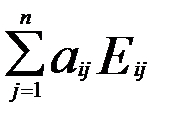

Насправді

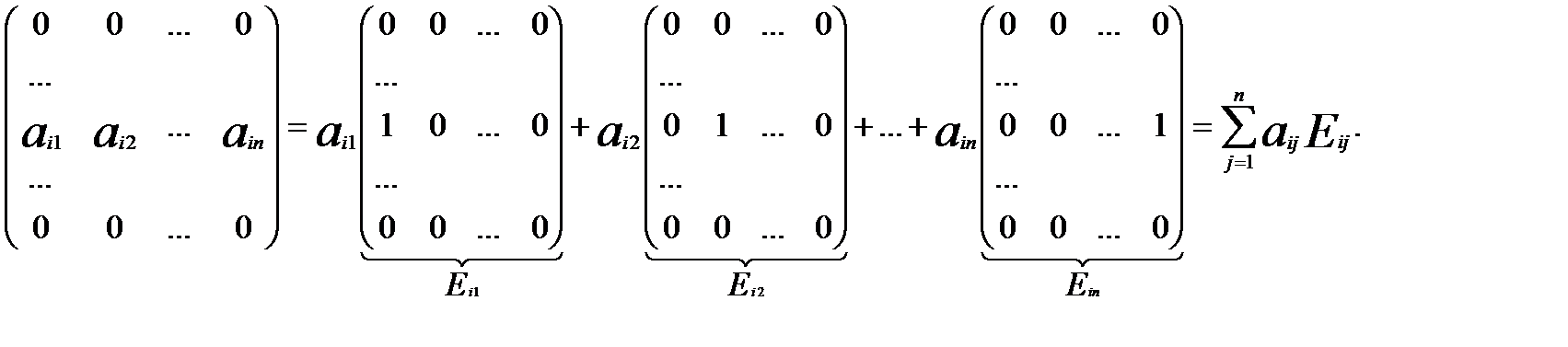
Розглянемо тепер матрицю А. Її можна подати у вигляді

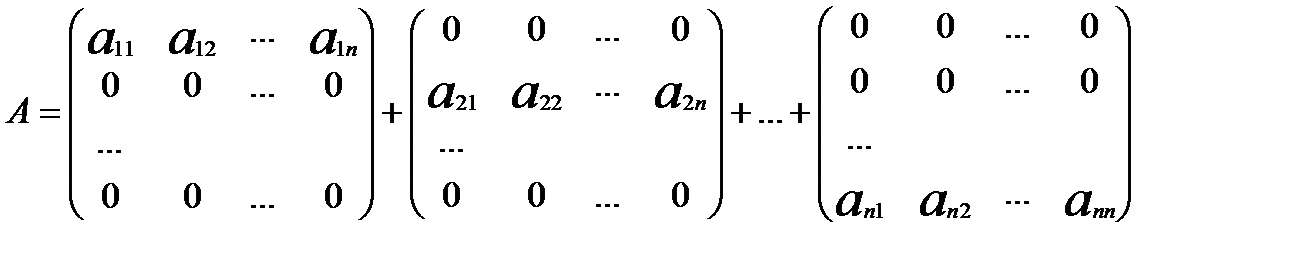
Застосуємо до кожного доданку попередню формулу

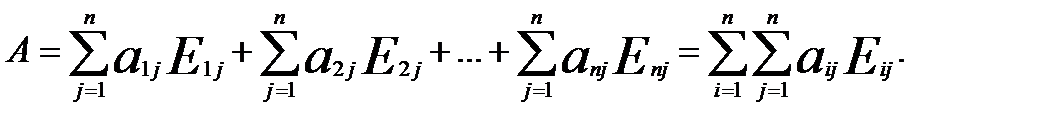
Вправа. Довести, що операція множення матриць і додавання матриць підпорядковується дистрибутивному закону:

А (В + С) = АВ + ВС.