 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Поняття і властивості визначника n-го порядку
|
|
На практичних заняттях було введено поняття визначника другого і третього порядків. Це були числа, отримані за певними законами з таких таблиць- матриць другого і третього порядків відповідно:
s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 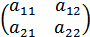
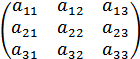
Визначник другого порядка – це число, що позначається 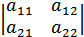 і яке дорівнює алгебраїчній сумі
і яке дорівнює алгебраїчній сумі 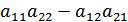 , аналогічно визначник третього порядку:
, аналогічно визначник третього порядку:
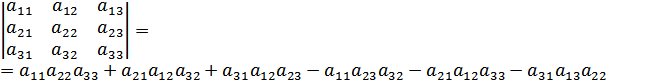
Ми хочемо узагальнити це поняття, тобто отримати визначник 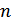 -го порядку таким чином, що з нього при
-го порядку таким чином, що з нього при 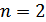 та
та 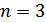 отримати попереднє.
отримати попереднє.
Аналіз обчислення визначників другого і третього порядків приводить до доцільності такого означення:
Означення. Визначником 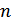 -го порядку, що відповідає матриці:
-го порядку, що відповідає матриці:

називається алгебраїчна сума 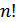 доданків, кожний з яких є добутком
доданків, кожний з яких є добутком 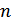 елементів, взятих по одному з кожного рядка і кожного стовпця матриці, причому зі знаком "+", якщо підстановка складена з перших і других індексів, парна і зі знаком "–", якщо вона непарна.
елементів, взятих по одному з кожного рядка і кожного стовпця матриці, причому зі знаком "+", якщо підстановка складена з перших і других індексів, парна і зі знаком "–", якщо вона непарна.
Отже визначник 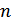 -го порядку складається з
-го порядку складається з 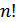 доданків вигляду
доданків вигляду 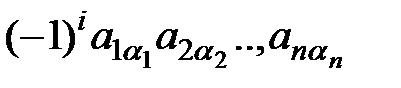 , де
, де 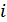 – кількість інверсій у перестановці α1,α2,…,αn.
– кількість інверсій у перестановці α1,α2,…,αn.
Для визначника вводять позначення:
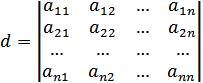
Властивість 1. Визначник не зміниться, якщо його рядки зробити відповідними стовпцями.
Розглянемо визначник d.
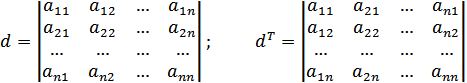
Стверджується, що 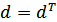
Розглянемо загальний член визначника d:
(1) 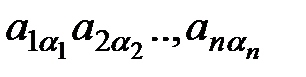 – загальний член d.
– загальний член d.
α1,α2,…,αn - перестановка з 1,2,…,n
Запишемо член (1) в позначках ij.
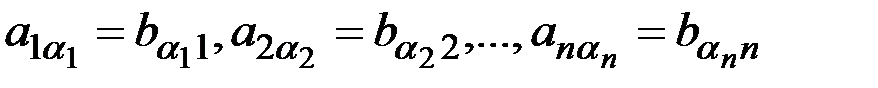
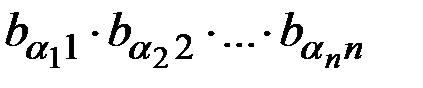 (1)
(1)
Таким чином (1) є членом і визначника d1. З′ясуємо, з яким знаком (1) входить до визначника d1. Знак члена (1) в d визначається парністю підстановки
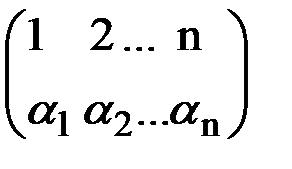
Знак (1) в d1 визначається парністю підстановки
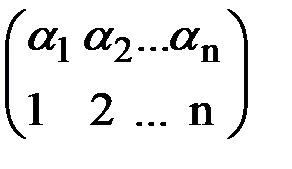
Ці підстановки, взагалі кажучи, різні, але парності в них однакові, тому що загальна кількість інверсій верхньої і нижньої перестановок однакова, тому і знаки члена (1) в d і d1 однакові.
Це перетворення, при якому всі рядки стають відповідними стовбцями, називається транспонуванням.
Властивість 2. Якщо в визначнику поміняти місцями будь які 2 рядки, то знак визначника зміниться на протилежний.
Доведення за схемою властивості 1.
Насправді, нехай у визначнику 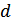 міняються місцями i-ий та j-ий рядки,
міняються місцями i-ий та j-ий рядки, 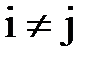 , а всі інші рядки залишаються на місці. Ми отримаємо визначник
, а всі інші рядки залишаються на місці. Ми отримаємо визначник 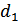 :
:
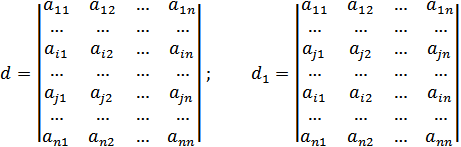 .
.
Якщо 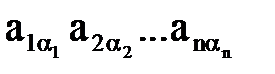 (1) є членом визначника
(1) є членом визначника 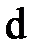 , то всі його елементи і у визначнику
, то всі його елементи і у визначнику 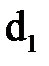 залишаються, очевидно, в різних рядках і різних стовпцях. Таким чином, визначники d та d1 складаються з одних і тих же членів.
залишаються, очевидно, в різних рядках і різних стовпцях. Таким чином, визначники d та d1 складаються з одних і тих же членів.
Члену (1) у визначнику 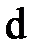 відповідає підстановка
відповідає підстановка 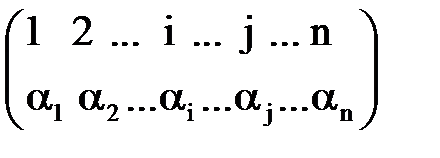 (2),
(2),
а у визначнику 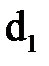 - підстановка
- підстановка 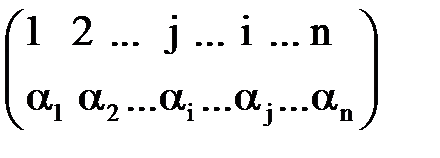 (3).
(3).
Підстановку (2) можна одержати з підстановки (1) однією транспозицією в верхньому рядку, тобто вона має протилежну парність. Звідси випливає, що всі члени визначника d входять до визначника d1 і відрізняються лише знаком.
Властивість 3. Якщо в визначнику є нульовий рядок, то визначник дорівнює 0.
Нехай усі елементи і-го рядка визначника є нулями
За означенням визначник n-го порядку це алгебраїчна сума n доданків, кожний з яких є добутком n елементів, узятих по одному з кожного рядка й кожного стовпця матриці і т.д. Отже, у кожний член визначника повинен увійти множником один елемент з і-ого рядка, тому в нашому випадку всі члени визначника дорівнюють нулю. Що й треба було довести.
Властивість 4. Якщо в визначнику є 2 рівних рядка, то визначник дорівнює 0.
Доведення. Нехай у визначнику d рівні між собою і-рядок і j=рядок
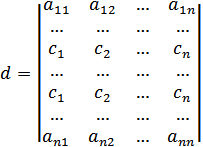
Нехай d = k
d1 – визначник d, в якому поміняли і з j рядок.
Тоді за властивістю 2:
d1=-k
Але насправді нічого не змінилось, оскільки, i та j рядки рівні
d1=d=k ⟹ -k=k
Звідси, 2k=0, k=0.
Властивість 5. Якщо всі елементи деякого рядка помножити на число r, то визначник зміниться в r разів.
Доведення за схемою властивості 1.
Цю ж властивість можна сформулювати у вигляді: якщо рядок визначника містить постійний множник, то його можна винести за знак визначника.
Розглянемо визначник d:
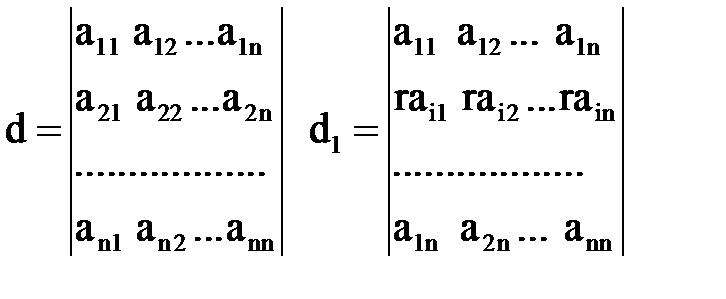
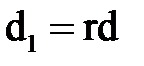
Нехай на r помножені всі елементи і-ого рядка. Кожний член визначника містить рівно один елемент із і-ого рядка, тому всілякий член отримує множник r, тобто сам визначник множиться на r.
Властивість 6. Якщо у визначнику є два пропорційні рядки, то визначник = 0.
Доведення проводиться з використанням властивості 5 і властивості 4.
Насправді, нехай елементи j-ого рядка визначника відмінюються від відповідних елементів і-ого рядка 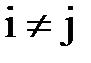 одним і тим самим множником r.
одним і тим самим множником r.
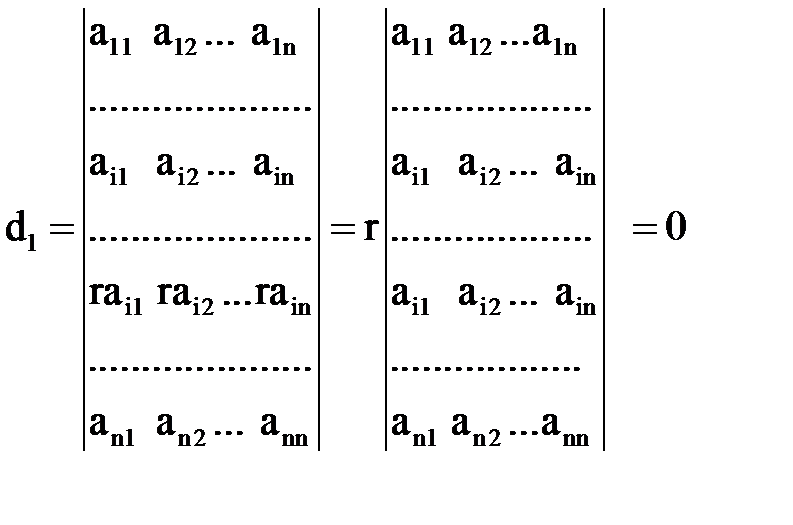
Виносячи спільний множник r із j-ого рядка за знак визначника, ми отримуємо визначник з двома однаковими рядками, який дорівнює нулю за властивістю 4.
Властивість 4 (а також властивість 3 при 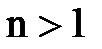 ) є, очевидно, окремим випадком властивості 6 (при r = 1 і r = 0).
) є, очевидно, окремим випадком властивості 6 (при r = 1 і r = 0).
Властивість 7. Якщо кожний елемент і-рядка визначників є сумою 2-ох доданків, то такий визначник можна подати як суму двох визначників, у яких всі рядки, за винятком і-ого такі ж, як у початковому. і-й рядок першого визначника складається з перших доданків, і-ий рядок другого визначника складається з других доданків.
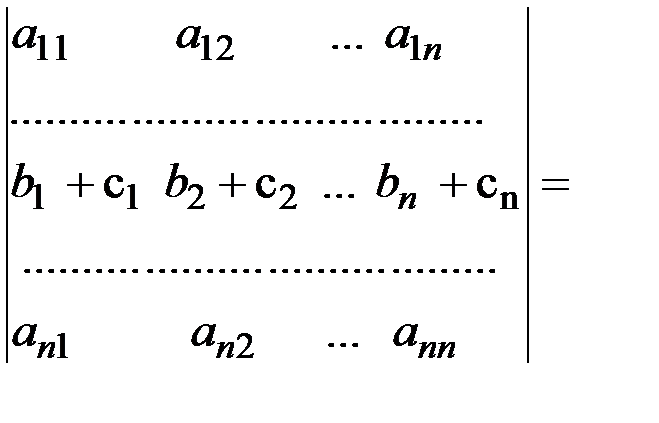
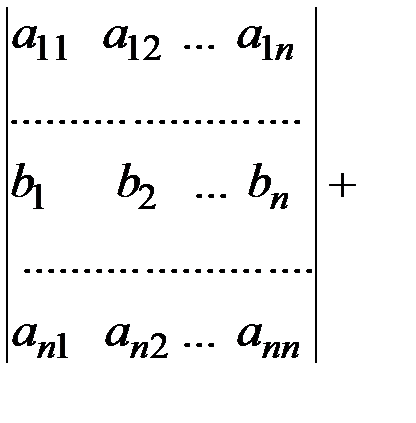

Доведення за схемою доведення властивості 1.
Дійсно, всілякий член заданого визначника можна подати у вигляді:
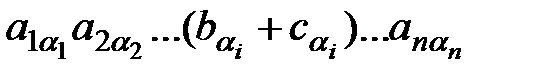
Збираючи разом перші доданки цих сум (з тими ж знаками, які мали відповідні члени в заданому визначнику) ми отримаємо, очевидно, визначник n-го порядку, що відмінюється від заданого визначника лише тим, що в і-ому рядку замість елементів 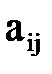 стоять елементи
стоять елементи 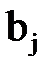 . Відповідно другі доданки складають визначник, в і-ому рядку якого стоять елементи
. Відповідно другі доданки складають визначник, в і-ому рядку якого стоять елементи 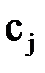 .
.
Властивість 8. Якщо до і-ого рядка визначника додати j-ий рядок, в подумках помножений на деяке число, то визначник не зміниться.
Доведення. Нехай до і-го рядка визначника d додається j-ий рядок, помножений на k, тобто в новому визначнику всілякий елемент і-го рядка має вигляд 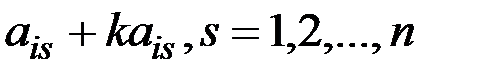 . Тоді на підставі властивості 7 цей визначник дорівнює сумі двох визначників, з яких перший є d, а другий містить пропорційні рядки і тому дорівнює 0.
. Тоді на підставі властивості 7 цей визначник дорівнює сумі двох визначників, з яких перший є d, а другий містить пропорційні рядки і тому дорівнює 0.
Властивість 9. Якщо в визначнику присутній рядок, що є лінійною комбінацією інших рядків, то визначник дорівнює 0.
Дата публикования: 2014-11-18; Прочитано: 6260 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
