Вiддаль вiд точки до площини

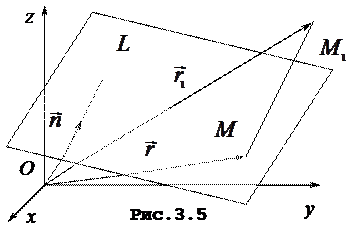Нехай площина Q задана своїм нормальним рiвнян-ням

i задана точка 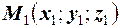. Потрiбно знайти вiддаль вiд точки до площини Q. Опустимо iз точки перпендикуляр на площину Q; його точка перетину з площиною Q - M. Iз нормального рiвняння площини Q виводимо, що

,

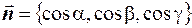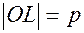
Розглянемо вектор 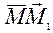i позначимо через d скалярний добуток векторiв .

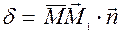d - це вiдхилення точки вiд площини Q, d >0, якщо точ-

ка i точка О розташованi по рiзнi сторони вiд площини Q i d<0 в протилежному випадку. Розглянемо ще радiус-век-тори 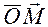та 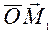. Тодi (рис. 3.5) .

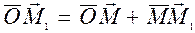Помножимо обидвi частини цiєї рiвностi скалярно на вектор .

.

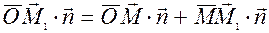Але ;

; .

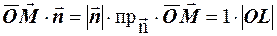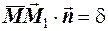Тодi

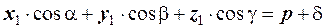; Вiддаль 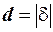. Звiдси

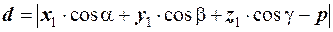(6*)

Для того, щоб знайти вiддаль вiд точки 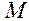₁ до площини Q, потрiбно в лiву частину нормального рiвняння площини Q замiсть поточних координат пiдставити координати точки i взяти цей вираз по модулю.

Якщо площина Q задана загальним рiвнянням (2*), то

(7*)