 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Алгоритмы генерирование некоторых случайных величин наиболее часто используемых распределений
|
|
4.9.1. Распределение Бернулли. Если дискретная случайная величина 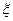 принимает только два значения (например, 0 и 1) с вероятностями
принимает только два значения (например, 0 и 1) с вероятностями 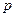 и
и 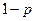 , то говорят, что она имеет распределение Бернулли с параметром
, то говорят, что она имеет распределение Бернулли с параметром 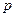 . В таком случае вводят обозначение
. В таком случае вводят обозначение 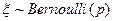 .
.
Алгоритм генерирования значений данной случайной величины эквивалентен алгоритму моделирования отдельного события, который приведен в пункте 6.3.1.
4.9.2. Биномиальное распределение. Биномиальное распределение вероятностей называется дискретное распределение случайной величины 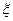 с параметрами
с параметрами 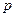 и
и 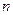
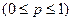 , принимающей целочисленные значения
, принимающей целочисленные значения 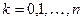 с вероятностями
с вероятностями
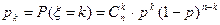 . Обозначают
. Обозначают 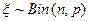 .
.
а) Непосредственное моделирование. Биномиальное распределение с параметрами 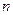 и
и 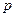 имеет вид
имеет вид
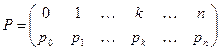
Применяем теорему 1.
Алгоритм непосредственного моделирования случайной величины 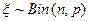 :
:
1. Моделируют случайную величину 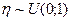 и в результате получают выборку объема
и в результате получают выборку объема 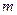 равномерно распределенных чисел на интервале (0;1):
равномерно распределенных чисел на интервале (0;1): 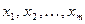 .
.
2. Формируют выборку объема 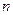 значений случайной величины
значений случайной величины 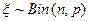 :
:
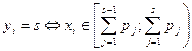 , где
, где 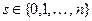 ,
, 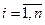 .
.
Дата публикования: 2014-11-18; Прочитано: 615 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
