 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Моделирование случайных событий
|
|
4.3.1. Моделирование отдельного события. Рассмотрим событие 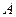 , которое происходит с вероятностью
, которое происходит с вероятностью 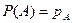 , и введем дискретную случайную величину
, и введем дискретную случайную величину 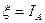 , где
, где 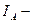 индикатор события
индикатор события 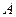 :
:
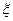
| ||
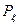
| 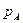
| 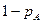 
|
Воспользуемся алгоритмом теоремы 1.
Тогда 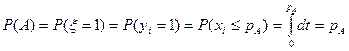 и
и 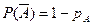 . Таким образом, генерируется последовательность
. Таким образом, генерируется последовательность 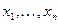 , являющаяся выборкой случайной величины
, являющаяся выборкой случайной величины 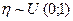 и данная выборка получена в результате независимых испытаний и в случае когда
и данная выборка получена в результате независимых испытаний и в случае когда
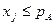 , (1)
, (1)
то полагаем, что в эксперименте событие 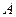 произошло, а в противном случае не произошло.
произошло, а в противном случае не произошло.
4.3.2. Моделирование полной группы событий. Рассмотрим полную группу попарно несовместных событий 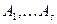 :
: 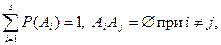 и
и 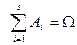 . Пусть
. Пусть 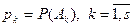 и случайная величина
и случайная величина 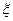 принимает значения равные номеру наступившего события:
принимает значения равные номеру наступившего события:
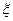
| 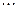
| s | ||
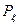
| 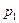
| 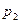
| 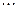
| 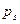
|
По алгоритму теоремы 1 получаем последовательность 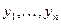 , где
, где 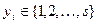 и в зависимости от конкретного значения
и в зависимости от конкретного значения 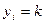 полагаем, что в опыте с номером
полагаем, что в опыте с номером 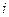 произошло событие
произошло событие 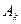 , а события
, а события 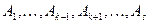 не произошли. Процедуру моделирования можно построить и используя последовательность равномерно распределенных чисел
не произошли. Процедуру моделирования можно построить и используя последовательность равномерно распределенных чисел 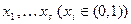 , так как
, так как 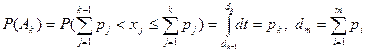 . И тогда исходом испытания
. И тогда исходом испытания 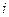 оказывается событие
оказывается событие 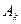 , если
, если
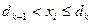 . (2)
. (2)
Данная процедура носит название – определение исхода испытания по жребию в соответствии с вероятностями 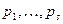 .
.
4.3.3. Моделирование двух независимых событий. Пусть события 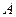 и
и 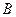 независимые и
независимые и 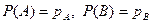 . Возможными исходами совместных испытаний могут быть следующие события
. Возможными исходами совместных испытаний могут быть следующие события 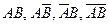 , с соответствующими вероятностями
, с соответствующими вероятностями
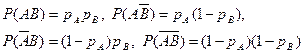 . (3)
. (3)
Тогда для моделирования совместных испытаний можно использовать два варианта:
- последовательную проверку условия (1) используя последовательности 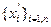 и
и 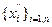 , соответственно для моделирования событий
, соответственно для моделирования событий 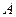 и
и 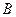 ;
;
- определения одного из исходов 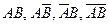 по жребию с соответствующими вероятностями (условия 2 и 3).
по жребию с соответствующими вероятностями (условия 2 и 3).
4.3.4. Моделирование двух зависимых событий. Рассмотрим случайные величины 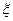 и
и 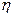 , которые являются индикаторами событий
, которые являются индикаторами событий 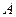 и
и 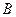 :
: 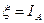 и
и 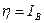 .
.
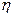
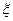
| ||
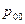
| 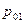
| |
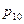
| 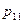
|
Где 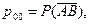
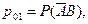
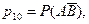
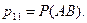 События
События 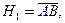
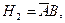
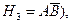 и
и 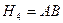 образуют полную группу несовместных событий.
образуют полную группу несовместных событий.
Введем новую случайную величину 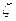 , принимающую значения номеров введенных событий
, принимающую значения номеров введенных событий 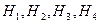 :
:
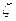
| ||||
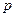
| 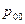
| 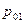
| 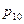
| 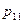
|
Применим алгоритм теоремы 1 для получения случайных чисел 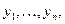
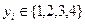 . Тогда, если
. Тогда, если 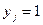 , то полагают, что в эксперименте
, то полагают, что в эксперименте 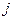 события
события 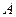 и
и 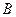 не произошли. В случае
не произошли. В случае 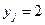 , то полагают, что в эксперименте
, то полагают, что в эксперименте 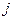 событие
событие 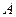 не произошло, а событие
не произошло, а событие 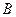 произошло. Если
произошло. Если 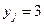 , то в эксперименте
, то в эксперименте 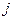 событие
событие 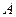 произошло, а событие
произошло, а событие 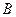 не произошло. И при
не произошло. И при 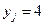 , полагают, что в эксперименте
, полагают, что в эксперименте 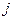 события
события 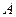 и
и 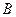 произошли.
произошли.
Рассмотрим другой вариант моделирования, когда нам известны вероятности событий 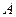 и
и 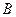 , а также условная вероятность наступления события
, а также условная вероятность наступления события 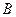 при условии, что
при условии, что 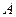 произошло -
произошло - 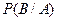 . Из последовательности
. Из последовательности 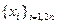 извлекаются два очередных числа
извлекаются два очередных числа 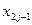 и
и 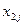
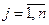 . Тогда, рассматривают четыре случая:
. Тогда, рассматривают четыре случая:
- если 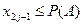 и
и 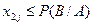 полагают наступление в
полагают наступление в 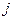 эксперименте события
эксперименте события 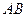 ;
;
- если 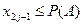 и
и 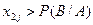 полагают наступление события
полагают наступление события 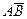 ;
;
- если 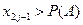 и
и 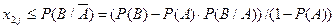 полагают, что в
полагают, что в 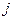 эксперименте произошло события
эксперименте произошло события 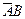 ;
;
- если 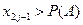 и
и 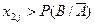 то произошло события
то произошло события 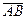 .
.
Дата публикования: 2014-11-18; Прочитано: 1018 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
