Моделирование однородной марковской цепи

Простая однородная цепь Маркова определяется матрицей переходов

,

где — вероятность перехода из состояния , в состояние и вектором начальных состояний , где .

Матрица переходов Р полностью описывает марковский процесс. Так как сумма элементов каждой строки равна 1, то данная матрица является стохастической, т. е. .

Пусть - вероятность, что система будет находиться в состоянии после 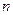переходов. По определению .

Пусть возможными исходами испытаний являются события и — это условная вероятность наступления события в данном испытании при условии, что исходом предыдущего испытания было событие 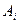. Моделирование такой цепи Маркова состоит в последовательном выборе событий по жребию с вероятностями .

Последовательность действий алгоритма следующая:

0) Подготовительный этап. Генерируем последовательность равномерно распределенных чисел на интервале (0;1):

(4)

1) Выбор начального состояния. Выбор начального состояния , задаваемого начальными вероятностями , осуществляется по алгоритму моделирования полной группы событий (см. 4.3.2). Из последовательности (4) выбирается число и определяется номер, 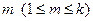для которого оказывается справедливым неравенство , где . Тогда начальным событием данной реализации цепи будет событие .

2) Определение первого перехода. Выбираем следующее случайное число 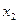, аналогично определяем номер следующего события, для которого оказывается справедливым неравенство , где . Таким образом, следующим событием данной реализации цепи будет событие .

в) Определение s-того перехода. Пусть в результате перехода произошло событие с номером : . Выбираем случайное число , определяем номер следующего события, для которого оказывается справедливым неравенство , где 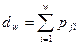. Таким образом, событием той реализацией цепи будет событие . И так далее.

Марковский процесс называют эргодическим, если предельное распределение вероятностей не зависит от начальных условий . Поэтому при моделировании эргодического Марковского процесса можно принять следующее условие