 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Моделирование многомерных случайных величин
|
|
4.8.1. Моделирование 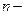 мерной случайной точки с независимыми координатами. Если координаты
мерной случайной точки с независимыми координатами. Если координаты 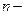 мерной случайной величины
мерной случайной величины  независимы, то функция распределения этой случайной величины равна
независимы, то функция распределения этой случайной величины равна
 ,
,
где 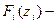 функция распределения случайной величины
функция распределения случайной величины  . Поэтому каждую величину
. Поэтому каждую величину  можно моделировать независимо по теореме 3 пункта 4.6.2:
можно моделировать независимо по теореме 3 пункта 4.6.2:
 . (2)
. (2)
Пример. Случайная точка  в декартовой системе координат равномерна распределена в
в декартовой системе координат равномерна распределена в 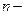 мерном параллелепипеде
мерном параллелепипеде 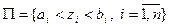 . Плотность вероятностей точки
. Плотность вероятностей точки  постоянна в
постоянна в  :
:

Интегрируя  по всем переменным, кроме
по всем переменным, кроме  , получим плотность случайной координаты
, получим плотность случайной координаты 

Тогда, согласно (2) запишем уравнение
 ,
,
откуда вытекают формулы для расчета координат случайной точки 
 .
.
Таким образом, посредством моделирования 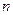 случайных величин
случайных величин  получают выборку равномерно распределенных чисел на интервале (0;1)
получают выборку равномерно распределенных чисел на интервале (0;1)  и вычисляют координаты точки
и вычисляют координаты точки 
 .
.
4.8.2. Моделирование 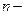 мерной случайной точки с произвольными координатами. В общем случае, когда
мерной случайной точки с произвольными координатами. В общем случае, когда 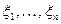 зависимы, их совместную плотность можно представить в виде произведения условных плотностей вероятностей этих величин:
зависимы, их совместную плотность можно представить в виде произведения условных плотностей вероятностей этих величин:
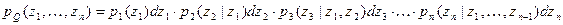
Все условные плотности вероятности выражаются через совместную плотность  :
:
 ,
,
 ,
,
 и т.д.
и т.д.
Тогда условная функция распределения будет представлена формулой

Теорема 6. Пусть  независимые случайные величины равномерно распределенные на интервале (0;1). Тогда совокупность случайных величин
независимые случайные величины равномерно распределенные на интервале (0;1). Тогда совокупность случайных величин 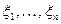 полученных при последовательном решении уравнений
полученных при последовательном решении уравнений
 (3)
(3)
имеет совместную плотность вероятностей  .
.
Доказательство. При фиксированных значениях  случайную величину
случайную величину  можно определить по формуле (5) пункта 4.6.2:
можно определить по формуле (5) пункта 4.6.2:
 .
.
Тогда вероятность неравенства  будет равна
будет равна
 .
.
Следовательно, с точностью до бесконечно малых более высокого порядка вероятность совместного выполнения 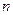 неравенств равна
неравенств равна
 Теорема доказана.
Теорема доказана.
Пример. Рассмотрим случайную точку  которая принимает значения в треугольнике
которая принимает значения в треугольнике  с плотностью
с плотностью  .
.
Совместную плотность для двух переменных можно представить двумя способами
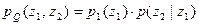 или
или  .
.
Рассмотрим эти два случая по отдельности. Для первого способа записи имеем
 , при
, при  ;
;
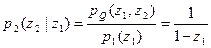 , при
, при  .
.
Находим соответствующие этим плотностям функции распределения:
 , при
, при  ;
;
 , при
, при  .
.
Из формул (3) данного пункта следует
 и
и  , где
, где  .
.
Для второго способа записи имеем
 , при
, при  ;
;
 , при
, при  .
.
Находим соответствующие этим плотностям функции распределения:
 , при
, при  ;
;
 , при
, при  .
.
Из формул (3) данного пункта следует
 и
и  , где
, где  .
.
Так как случайные величины  и
и  эквиваленты, то можно
эквиваленты, то можно  заменить на
заменить на  и в итоге получим
и в итоге получим
 и
и  , где
, где  .
.
Дата публикования: 2014-11-18; Прочитано: 1151 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
