Апериодическое звено второго порядка

Характеристическое уравнение звена следующее:

.

Уравнение имеет действительные отрицательные корни:

.

Данное звено можно представить в виде последовательно соединенных звеньев с различными постоянными времени:

где

Тогда, при переходная характеристика звена имеет вид:

.

Апериодическое звено II порядка не является элементарным, поскольку представляет собой последовательное соединение двух апериодических звеньев первого порядка с постоянными времени и .

То есть в решении присутствуют затухающие экспоненты. Типичное поведение звена с такими параметрами показано на рис. 3.27.

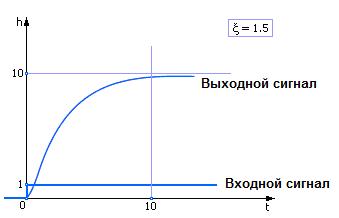
Рис. 3.27. Реакция апериодического звена
на единичный входной сигнал

В частном случае, когда , оба корня будут одинаковыми, отрицательными

.

Колебательное звено второго порядка .

Характеристическое уравнение звена следующее:

.

Корни разные, комплексно-сопряженные, с отрицательной вещественной частью:

,

где .

Так как корни мнимые, то в поведении звена присутствует колебательная составляющая. Именно за эту особенность поведения звено получило название колебательного. Колебательность звена особенно

выражена при малых значениях параметра затухания (см. рис. 3.28 и рис. 3.29).

Рис. 3.28. Переходная функция колебательного звена

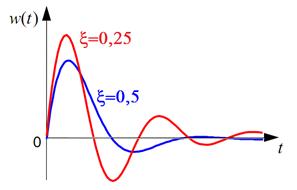
Рис. 3.29. Весовая функция колебательного звена

Из графиков видно, что с ростом ξ колебательность звена уменьшается, исчезая при ξ ≥ 1.

Переходная функция звена имеет вид:

где

При малых ξ значение A приближается к 1, а значение φ — к 90°. По физическому смыслу ω ₀ представляет собой собственную частоту колебаний.

Консервативное звено второго порядка .

Характеристическое уравнение звена следующее:

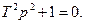
Корни одинаковые, комплексно-сопряженные, с нулевой вещественной частью:

.

Так как корни чисто мнимые, то поведением звена являются незатухающие колебания (ξ = 0), см.рис. 3.30.

Рис. 3.30. Реакция колебательного звена на

входной единичный сигнал (ξ = 0)

Переходная функция звена имеет вид: h (t) = k · (1 – cos(t / T)).

Из графика экспериментальным путем можно определить единственный параметр T = T ₀/(2 · π).