Б) частотные характеристики

Частотные характеристики описывают передаточные свойства системы

в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием.

Пусть на вход системы в момент времени подано гармоническое воздействие определенной частоты и амплитуды

. (3.19)

Через некоторое время, необходимое для протекания переходного процесса, система войдет в режим установившихся вынужденных колебаний, а выходная величина будет изменяться по гармоническому закону с той же частотой , но с отличающейся амплитудой и со сдвигом по оси времени

, (3.20)

где - период колебаний;

- фазовый сдвиг между входным и выходным сигналами.

Рис.3.7.

Повторяя такой эксперимент при фиксированном значении для различных значений частоты (от 0 до ∞), можно установить, что амплитуда и фазовый сдвиг выходного сигнала конкретной системы зависят от частоты воздействия.

На практике для получения гармонического сигнала используется генератор синусоидальных колебаний.

Подавая гармоническое воздействие на вход различных систем, можно убедиться, что величины и зависят также от типа и параметров систем.

Так как амплитуда выходного сигнала зависит еще от амплитуды входного сигнала, то целесообразно при описании передаточных свойств систем рассматривать отношение амплитуд .

Зависимость отношения амплитуд выходного и входного сигнала от частоты называют амплитудной частотной характеристикой (сокращено – АЧХ) и обозначают (см. рис.3.8,а).

Зависимость фазового сдвига между входным и выходным сигналами от частоты называют фазовой частотной характеристикой (сокращено – ФЧХ) и обозначают (см. рис.3.8,б).

Аналитические выражения и называют соответственно амплитудной и фазовой частотными функциями.

Рис.3.8.

АЧХ показывает, как система пропускает сигналы различной частоты. Оценка пропускания производится по отношению амплитуд . ФЧХ показывает, какое отставание или опережение выходного сигнала по фазе создает система при различных частотах в установившемся режиме.

Амплитудную и фазовую частотные характеристики можно объединить в одну общую – амплитудно-фазовую частотную характеристику (АФЧХ).

Амплитудно-фазовая частотная характеристика W (jω) представляет собой функцию комплексного переменного jω, модуль которого равен , а аргумент .

Каждому фиксированному значению частоты соответствует комплексное число , которое на комплексной плоскости можно изобразить вектором, имеющим длину и угол поворота (см. рис.3.9).

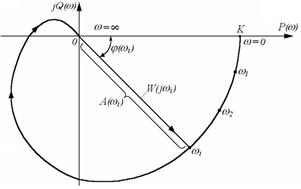
Рис.3.9.

Отрицательные значения , соответствующие отставанию выходного сигнала от входного, принято отсчитывать по часовой стрелке от положительного направления действительной оси.

При изменении частоты от нуля до бесконечности вектор поворачивается вокруг начала координат, при этом одновременно увеличивается или уменьшается длина вектора. Кривая, которую при этом опишет конец вектора, называемая годографом Найквиста, и есть АФЧХ. Каждой точке характеристики соответствует определенное значение частоты.

Проекции вектора на действительную и мнимую оси называют соответственно действительной и мнимой частотными характеристиками и обозначают

.

Аналитическое выражение для АФЧХ можно получить из передаточной функции путем подстановки

.

АФЧХ , как и любая комплексная величина, может быть представлена:

· в показательной форме ,

где -модуль АФЧХ;

- модуль сдвига по фазе;

· алгебраической ;

· в тригонометрической .

Связь между различными частотными функциями следующая:

Часто представляет собой дробь

.

Тогда используя известные в теории комплексных чисел соотношения, получим

Пример. Определить сигнал на выходе системы по известному входному сигналу и передаточной функции

Решение. Известно, что при воздействии входного сигнала на систему выходной сигнал по истечении времени переходного процесса также будет гармоническим, но отличаться от входного сигнала амплитудой и фазой

,

где - АЧХ системы;

- ФЧХ системы.

Следовательно, для определения необходимо найти и . По передаточной функции находим

На частоте

Тогда .

Частотные характеристики во многих случаях можно снять экспериментально. Если объект устойчивый, на его вход подается гармонический сигнал (3.19) и записывается сигнал на выходе (рис.3.10). Определив амплитуду и сдвиг фазы для разных частот, можно построить по точкам АФЧХ.

Рис.3.10.

Если объект неустойчив, то при подаче на вход синуса амплитуда колебаний на выходе будет неограниченно расти.