Б) апериодическое (инерционное) звено первого порядка

Дифференциальное уравнение звена имеет вид

. (3.23)

У такой системы два параметра:

T – постоянная времени, характеризующая инерционность звена (его пропускную способность);

k – безразмерный передаточный коэффициент, характеризующий свойства звена в статическом режиме.

В качестве примера апериодического звена можно привести 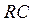- цепочку (рис. 3.21).

Рис.3.21. RC-цепочка

Если за входное воздействие принять напряжение , а за выходной сигнал . Тогда связь между ними задается уравнением:

.

Здесь постоянная времени , а коэффициент . Размерность постоянной времени [ 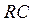]=сек. Коэффициент усиления в силу одинаковой природы входного выходного сигналов безразмерен и равен в данном случае единицы.

Найдем переходную функцию этого звена. Решая уравнение (3.23) при , получим (находится как сумма общего и частного решений)

,

где С – константа (должна определяться из начальных условий).

Поскольку нас интересует переходная характеристика, начальные условия считаем нулевыми, то есть , что дает и поэтому

. (3.24)

Переходная характеристика звена представлена на рис.3.22.

Рис.3.22

Обратите внимание, что предельное значение переходной характеристики равно k, а касательная к ней в точке t =0 пересекается с линией установившегося значения при t = Т. Переходная и импульсная характеристики выходят на установившееся значение (с ошибкой не более 5%) примерно за время . Эти факты позволяют определить постоянную времени экспериментально, по переходной характеристике звена.

На рис.3.23 показаны переходные характеристики (3.24) при различных значениях параметра Т, который называется постоянной времени звена.

Рис.3.23. Выходной сигнал, типичный для

инерционного звена первого порядка

Из рисунка видно, что при увеличении Т выход у медленнее достигает установившегося значения, равного k, т.е. постоянная времени характеризует инерционность звена (3.23). Чем больше постоянная времени, чем медленнее реагирует система на управление, тем больше усилий необходимо для того, чтобы перевести ее в новое состояние.

При малой величине T система слабо зависит от начальных условий, и вход мгновенно заставляет измениться выход.

При очень большом значении T система выдает неизменный выходной сигнал, практически не реагируя на входные воздействия.

Переходной процесс считается законченным при .

Дифференцируя переходную характеристику (3.24), получаем соответствующую импульсную характеристику

.

Рис.3.24.

Передаточная функция W (p)

. (3.25)

Частотная характеристика

.

Здесь

.

На рис.3.25 представлен годограф частотной характеристики – это полуокружность с центром в точке (0,5 k; 0) радиуса 0,5 k. Годограф начинается (на нулевой частоте) в точке (k; 0) и заканчивается в начале координат (при ).

Рис.3.25

Поскольку АФЧХ уменьшается на высоких частотах, инерционное звено подавляет высокочастотные шумы, т.е. обладает свойством фильтра низких частот.

Для сравнения рассмотрим также неустойчивое звено первого порядка, которое задается уравнением

. (3.26)

Как видим, все отличие от (3.23) – только в знаке в левой части уравнения (плюс сменился на минус). Однако при этом кардинально меняются переходная и импульсная характеристики:

,

Переходная функция звена (3.26) представлена на рис.3.26.

Рис.3.26.

Обычно предполагается, что постоянная времени Т > 0, тогда экспоненты в выражениях бесконечно вырастают с ростом t. Поэтому звено названо «неустойчивом»: в покое оно находиться в неустойчивом положении, а при малейшем возмущении «идет вразнос».

в) колебательное звено (инерционное звено второго порядка)

Такие звенья описываются дифференциальным уравнением вида

, (3.27)

где - постоянная времени колебательного звена;

- коэффициент демпфирования звена (или коэффициент

затухания);

- коэффициент усиления звена.

В зависимости от величины коэффициента демпфирования различают четыре типа звеньев:

a) колебательное звено ;

b) апериодическое звено второго порядка ;

c) консервативное звено ;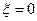

d) неустойчивое колебательное звено .

Преобразуем (3.27) по Лапласу

или, иначе:

. (3.28)

Определим передаточную функцию звена

.

Если записать уравнение (3.28) без входного воздействия (нулевые входные воздействия X (p)= 0) и сократить Y (p), то есть: , то такое уравнение будет называться характеристическим, поскольку характеризует исключительно внутренние свойства звена.