Б) получение моделей систем на основе уравнения Лагранжа

Модели в форме уравнений Лагранжа часто используются для описания механических систем. Рассмотрим простейшую механическую систему, изображённую на рис.3.3, которая представляет собой абсолютно твёрдое тело, движущееся по гладкой поверхности вдоль оси x. Тело с

одной стороны крепится к стенке с помощью пружины. Силы сопротивления внешней среды (например, трения) не учитываются.

Рис.3.3. Модель движения твердого тела под действием пружины

В соответствии со вторым законом Ньютона уравнение движения тела:

, (3.2)

где - сила со стороны пружины с коэффициентом жесткости (в

общем случае );

m – масса тела;

Тело находится в поле потенциальной силы пружины, - потенциальная сила, которая в соответствии с законом Гука (Hooke) всегда направлена противоположно движению тела.

Потенциальные силы П (консервативные силы) - силы, работа которых зависит только от начального и конечного положений точки и не зависит ни от вида траектории этой точки, ни от закона её движения. Работа потенциальных сил вдоль произвольной замкнутой траектории всегда равна нулю. Поле потенциальных сил характеризуется скалярным потенциалом. Потенциальная сила F, действующая на материальную точку, равна взятому с обратным знаком градиенту потенциальной энергии П этой точки в поле силы F, т.е. .

Кинетическая энергия T движущегося тела с массой m равна

. (3.3)

Потенциальная энергия П движущегося тела, находящегося в поле действия силы пружины, равна

. (3.4)

Закон сохранения полной энергии механической системы без потерь,

находящейся в поле потенциальных сил, выражается формулой

. (3.5)

Равенство (3.3) можно продифференцировать по :

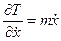. (3.6)

При дифференцировании (3.6) по переменной t получаем выражение

. (3.7)

Равенство (3.4) можно продифференцировать по :

. (3.8)

С учетом выражения (3.2) получаем уравнение

. (3.9)

Уравнение (3.9) представляет собой специальный (частный) случай уравнения движения Лагранжа с одной степенью свободы.

В общем случае уравнения движения Лагранжа 2-го рода для систем

без потерь (консервативных систем) записываются в следующем виде:

(3.10)

где .

В аналитической механике переменные и принято называть обобщенными координатами и обобщенными скоростями, а присутствующие в правых частях обобщенные силы являются потенциальными (консервативными) и определяются выражениями:

.

Система (3.10) характеризуется n степенями свободы.

Введем функцию Лагранжа (лагранжиан) системы

, (3.11)

где .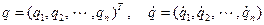

Как видно из (3.11), кинетическая энергия, в общем случае, зависит как от , так и от , тогда как потенциальная – только от .

С учетом (3.11) уравнение Лагранжа (3.10) для консервативной системы при отсутствии внешних (неконсервативных) сил можно записать в виде однородных дифференциальных уравнений

. (3.12)

Из выражения (3.11) следует, частные производные лагранжиана равны

(3.13)

С помощью этих формул устанавливается связь между лагранжианом L, кинетической Т и потенциальной П энергиями.

Пример. Рассмотрим простейшую модель механической системы колебания математического маятника в потенциальном поле сил

тяжести. Система представляет собой груз массы m, находящийся на кон-

це стержня длины l. Рассматриваемая система может совершать плоские свободные колебания (рис. 3.4).

Рис. 3.4. Модель колебаний математического маятника

Относительно изучаемой системы делаются следующие предположения. Шарнир считается идеально гладким (трение в нём отсутствует). К тому же он неподвижен, т.е. энергия от него не поступает в систему «стержень-груз». Следовательно, шарнир не способен совершать над системой какую-либо работу. Стержень невесом и абсолютно жёсткий. Поскольку геометрический размер груза пренебрежимо мал по сравнению с длиной стержня l, груз можно заменить материальной точкой. Ускорение свободного падения g постоянно, сопротивление воздуха исключено.

Требуется получить описание движения системы с помощью уравнений Лагранжа.

С учётом сделанных предположений, можно считать, что положение маятника в плоскости совершаемых колебаний определяется одной обобщённой координатой, в качестве которой выбирается угол отклонения маятника от вертикали, т.е. . Тогда обобщенной скоростью можно считать угловую скорость .

Кинетическая энергия системы, записанная через линейную скорость , определяется выражением

.

Потенциальная энергия системы, принимая во внимание, что отклонение маятника по вертикали относительно нижнего положения определяется значением h, равна

.

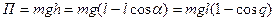Тогда лагранжиан системы имеет вид

.

В результате дифференцирования L по обобщенным координатам и

,

а также дифференцирования по переменной t

,

уравнение Лагранжа принимает окончательный вид

.

Для систем с потерями (диссипативные системы) уравнения Лагранжа приобретают вид

,

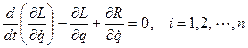где функцию R называют диссипативной функцией Рэлея (Rayleigh) (функцией рассеивания).

Диссипативная функция Рэлея определяется выражением

, (3.14)

Отсюда

,

где - i -я сила трения, приложенная к системе;

- i -й коэффициент трения.