 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Функциональные ряды
|
|
Определение 3.1. Пусть функции  определены в области
определены в области  . Тогда выражение вида
. Тогда выражение вида
 (3.1)
(3.1)
называется функциональным рядом.
Придавая 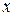 определенные значения
определенные значения  , получаем числовой ряд
, получаем числовой ряд
 ,
,
который может быть как сходящимся, так и расходящимся.
Определение 3.2. Если числовой ряд  сходится при
сходится при  , то ряд называется сходящимся в точке
, то ряд называется сходящимся в точке  , а сама точка
, а сама точка  называется точкой сходимости ряда. Множество значений
называется точкой сходимости ряда. Множество значений 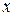 , при которых ряд (7.1) сходится, называется областью сходимости функционального ряда.
, при которых ряд (7.1) сходится, называется областью сходимости функционального ряда.
Область сходимости функционального ряда обозначим  . Как правило, область
. Как правило, область  не совпадает с областью
не совпадает с областью  , а является ее подмножеством, т.е.
, а является ее подмножеством, т.е. 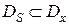 .
.
Пример 3.1. Найти область сходимости функционального ряда
 .
.
Решение. Область определения функций – это  .
.
Данный ряд является членом геометрической прогрессии со знаменателем  . Такой ряд сходится, если
. Такой ряд сходится, если  .
.
 Û
Û  Û
Û  .
.
Поэтому область сходимости исследуемого ряда является интервал  . Таким образом,
. Таким образом, 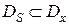 .
.
,
Так как каждому  соответствует некоторое число – сумма числового ряда, то указанное соответствие определяет функцию
соответствует некоторое число – сумма числового ряда, то указанное соответствие определяет функцию 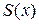 , которая называется суммой ряда (3.1) в области
, которая называется суммой ряда (3.1) в области  . Сумма функционального ряда в области сходимости
. Сумма функционального ряда в области сходимости  определяется равенством
определяется равенством
 ,
,
где  -
- 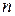 - я частичная сумма функционального ряда.
- я частичная сумма функционального ряда.
В таком случае  - есть
- есть 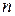 - й остаток функционального ряда. В области сходимости ряда
- й остаток функционального ряда. В области сходимости ряда  .
.
Пример 3.2. Найти область сходимости и сумму функционального ряда
 .
.
Решение. Данный ряд является рядом геометрической прогрессии со знаменателем  . Следовательно, этот ряд сходится при
. Следовательно, этот ряд сходится при  , т.е. при всех
, т.е. при всех 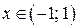 . Таким образом, область сходимости
. Таким образом, область сходимости  .
.
В области сходимости данного функционального ряда найдем сумму. По формуле суммы геометрической прогрессии при  получаем
получаем
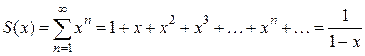 , при
, при  .
.
,
Дата публикования: 2014-11-19; Прочитано: 1926 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
