Свойства степенных рядов

Сформулируем без доказательства основные свойства степенных рядов.

1. Сумма 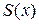степенного ряда (3.3) является непрерывной функцией в интервале сходимости .
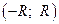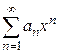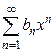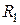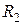2. Степенные ряды и , имеющие радиусы сходимости соответственно и , можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из числе 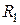и .
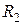3. Степенной ряд внутри интервала сходимости можно почленно дифференцировать. Для ряда

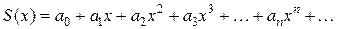
при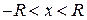

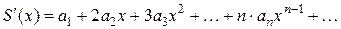. (3.6)

1. Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости. Для ряда (7.3) при 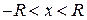выполняется равенство

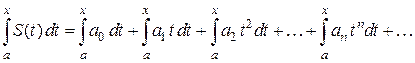. (3.7)

Ряды (3.6) и (3.7) имеют тот же радиус сходимости, что и исходный степенной ряд.

Перечисленные свойства остаются справедливыми и для степенных рядов вида (3.2).

Пример 3.8. Найти сумму ряда

.

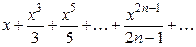Решение. Найдем интервал сходимости данного ряда. Используя признак Даламбера, получаем

.

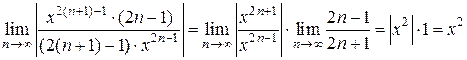Для того, чтобы ряд сходился, необходимо выполнение следующего равенства:

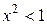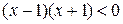Û Û .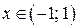

Таким образом, интервал сходимости есть .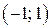

Так как ряд сходится при 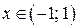, то его можно почленно дифференцировать в интервале сходимости. Обозначив сумму ряда через 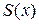, имеем

.

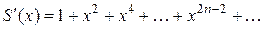В интервале сходимости полученный ряд есть сумма членов убывающей геометрической прогрессии со знаменателем 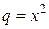и его сумма 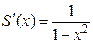. Проинтегрировав ряд из производных на отрезк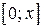е , где 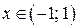найдем сумму данного ряда:

.

,