Признак Даламбера

В отличие от признаков сравнения, где все зависит от догадки и запаса известных сходящихся и расходящихся рядов, признак Даламбера (1717 – 1783, французский математик) позволяет часто решать вопрос о сходимости ряда, проделав лишь некоторые операции над самими рядами.

Теорема 1.5 (признак Даламбера). Пусть дан ряд (1.1) с положительными членами и существует конечный или бесконечный предел

.

Тогда:

1) при ряд сходится;

2) при ряд расходится.

При признак Даламбера не дает ответа на вопрос о сходимости или расходимости ряда. В этом случае сходимость ряда исследуется с помощью других признаков.

Признак Даламбера целесообразно применять, когда общий член ряда содержит выражения вида 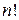или .

Пример 1.8. Исследовать на сходимость ряд .

Решение. Применим признак Даламбера:

, .

Находим

.

Так как , то данный ряд по признаку Даламбера сходится.,

Пример 1.9. Исследовать на сходимость ряд .

Решение. Применим признак Даламбера:

, .

Находим

.

Так как , то данный ряд по признаку Даламбера расходится.

,