 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Признак Лейбница
|
|
Рассмотрим важный класс рядов, у членов которых поочередно изменяются знаки. Такие ряды называются знакочередующиеся.
Определение 2.1. Знакочередующимся рядом называется ряд вида
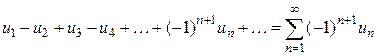 , (2.1)
, (2.1)
где 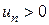 для всех
для всех 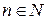 (т.е. ряд, положительные и отрицательные члены которого следуют друг за другом поочередно).
(т.е. ряд, положительные и отрицательные члены которого следуют друг за другом поочередно).
Для знакочередующихся рядов имеет место достаточный признак сходимости, установленный в 1714 г. Лейбницем в письме к И.Бернулли.
Теорема 2.1 (признак Лейбница). Знакочередующийся ряд (2.1) сходится, если
1) последовательность абсолютных величин ряда монотонно убывает, т.е.
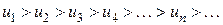 ;
;
2) общий член ряда стремится к нулю, т.е.
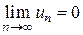 .
.
При этом сумма  ряда (2.1) удовлетворяет неравенствам
ряда (2.1) удовлетворяет неравенствам 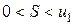 .
.
Следствие. Остаток 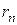 ряда (2.1) по абсолютной величине меньше абсолютной величины первого из отбрасываемых членов, т.е.
ряда (2.1) по абсолютной величине меньше абсолютной величины первого из отбрасываемых членов, т.е.
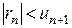 .
.
Например, по признаку Лейбница ряд
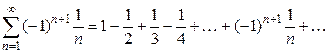
сходится, т.к. выполняются условия теоремы 2.1:
1) 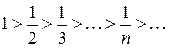 ; 2)
; 2) 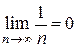 .
.
Дата публикования: 2014-11-19; Прочитано: 619 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
