Интегральный признак Коши

Теорема 1.7 (интегральный признак Коши). Пусть дан ряд

,

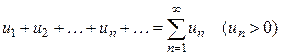члены которого являются значениями непрерывной положительной функции при целых значениях аргумента :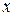

,

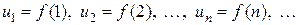и пусть монотонно убывает на промежутке 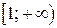. Тогда ряд сходится, если сходится несобственный интеграл 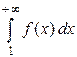, и расходится, если несобственный интеграл 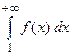расходится.

Надо отметить, что вместо интеграла 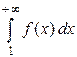можно брать интеграл 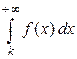, где 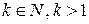. Отбрасывание 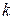первых членов ряда, как известно, не влияет на сходимость (расходимость) ряда.

Пример 1.11. Исследовать на сходимость ряд

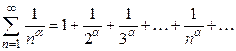, (1.10)

где 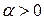- действительное число, ряд называется обобщенным гармоническим рядом или рядом Дирихле.

Решение. Рассмотрим функцию 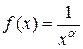, которая непрерывна и монотонно убывает на промежутке 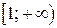, при 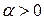. Воспользуемся интегральным признаком Коши и исследуем на сходимость несобственный интеграл .

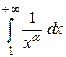При 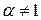имеем

.

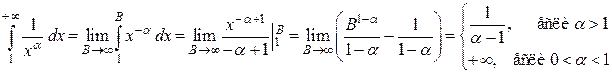При 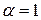получаем гармонический ряд 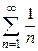, который расходится.

Таким образом, при 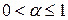ряд Дирихле расходится, а при 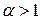ряд Дирихле сходится.

,

Пример 1.12. Исследовать на сходимость ряд .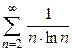

Решение. Воспользуемся интегральным признаком Коши. Рассмотрим функцию 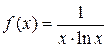, которая непрерывна и монотонно убывает на промежутке 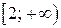. Находим

.

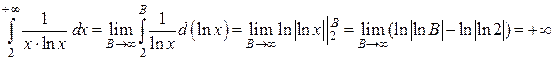Поскольку несобственный интеграл расходится, то и исходный ряд расходится.

,

Пример 1.13. Исследовать на сходимость ряд .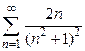

Решение. Воспользуемся интегральным признаком Коши. Рассмотрим функцию 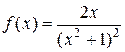, которая непрерывна и монотонно убывает на промежутке .

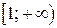Находим

.

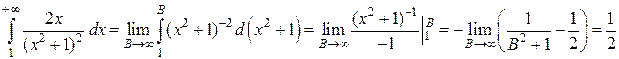Поскольку несобственный интеграл сходится, то и исходный ряд сходится.

,

2. ЗНАКОЧЕРЕДУЮЩИЕСЯ И

ЗНАКОПЕРЕМЕННЫЕ РЯДЫ