Необходимый признак сходимости ряда

Основные понятия

Бесконечные ряды широко используются в теоретических исследованиях математического анализа, имеют разнообразные практические применения.

Определение 1.1. Числовым рядом (или просто рядом) называется выражение вида

, (1.1)

где - члены ряда (действительные или комплексные числа), число - общий член ряда.

Ряд считается заданным, если известно правило, по которому для любого номера 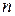можно записать соответствующий член ряда: , т.е. при помощи формулы 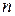-го члена.

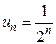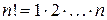Если формула дана, то можно сразу написать любой член ряда. Например, если , то ряд имеет вид: . Если (), то ряд имеет вид: .

Иногда ряд задается при помощи рекуррентного соотношения, связывающего последующий член ряда с предыдущим. При этом задается несколько первых членов ряда и формула, по которой находятся следующие члены ряда. Например, пусть , а рекуррентная формула такова: . Последовательно находим ; и т.д. Таким образом, получаем ряд: .

Определение 1.2. Сумма конечного числа 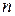первых членов ряда называется 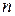-й частичной суммой ряда:

.

Рассмотрим частичные суммы

,

,

………………….

Если существует конечный предел , то этот предел называют суммой ряда (1.1) и говорят, что ряд сходится. Если не существует или , то ряд (1.1) расходится и суммы не имеет. Например, ряд сходится и его сумма равна 0; ряд 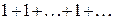расходится, так как при ; ряд расходится, так как последовательность частичных сумм не имеет предела.

Пример 1.1. Дан ряд . Установить сходимость этого ряда и найти его сумму.

Решение. Запишем 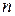-ю частичную сумму данного ряда и преобразуем ее:

.

Поскольку

,

то данный ряд сходится и его сумма .

,

Пример 1.2. Исследовать сходимость ряда

, (1.2)

который называется геометрической прогрессией.

Решение. Сумма 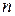первых членов прогрессии находится по формуле

или

.

1) Если , то при , следовательно

.

Значит, в случае ряд (1.2) сходится и его сумма .

2) Если , то при . Поэтому . А значит, в случае ряд (1.2) расходится.

3) Если 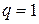, то ряд (1.2) имеет следующий вид: . В этом случае , следовательно , т.е ряд расходится.

4) Если , то ряд (1.2) имеет вид: . В этом случае

.

Следовательно, предела не имеет – ряд расходится.

Итак, ряд геометрической прогрессии сходится при и расходится при .

,

Рассмотрим некоторые важные свойства рядов (без доказательства).

1. Если ряд (1.1) сходится и его сумма равна , то ряд

, (1.3)

где - произвольное число, также сходится и его сумма равна . Если же ряд (1.1) расходится и , то и ряд (1.3) расходится.

1. Если ряды

и

сходятся и их суммы соответственно равны и 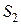, то ряды

(1.4)

и

(1.5)

также сходятся и их суммы соответственно равны и .

3. Если к ряду (1.1) прибавить (или отбросить) конечное число членов, то полученный ряд и ряд (1.1) сходится или расходится одновременно.

Рассмотрим сходящийся ряд (1.1)

.

Разность между суммой ряда и его 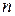-й частичной суммой называется 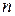-м остатком ряда. Остаток ряда есть в свою очередь сумма бесконечного ряда. Обозначим остаток ряда 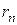. Тогда имеем

. (1.6)

Если ряд (1.1) сходится, то .

Необходимый признак сходимости ряда

Нахождение 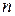-й частичной суммы и ее предела для произвольного ряда во многих случаях является непростой задачей. Поэтому для выяснения сходимости ряда устанавливают специальные признаки сходимости. Первым из них, как правило, является необходимый признак сходимости.

Теорема 1.1. (необходимый признак сходимости ряда) Если ряд (1.1) сходится, то его общий член стремится к нулю, т.е. .

Доказательство. Пусть ряд (1.1) сходится и . Тогда (при и ). Учитывая, что при , получаем:

.

,

Теорема 1.2. (достаточный признак расходимости ряда) Если или этот предел не существует, то ряд расходится.

Теорему 1.2. примем без доказательства.

Пример 1.3. Исследовать сходимость ряда .

Решение. Данный ряд расходится, так как

,

т.е. выполняется достаточное условие расходимости ряда.

,

Пример 1.4. Исследовать сходимость ряда

.

Решение. Данный ряд расходится, так как

,

,

Теорема 1.1 дает необходимое условие сходимости ряда, но не достаточное: из условия не следует, что ряд сходится. Это означает, что существуют расходящиеся ряды, для которых .

Например, гармонический ряд

(1.7)

общий член стремится к нулю, однако ряд расходится.