Основные свойства определённого интеграла

1. Определенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определенных интегралов от слагаемых функций: .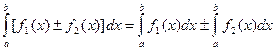

2. Постоянный множитель можно выносить за знак определенного интеграла: .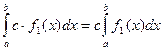

3. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный: .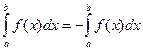

4. Определенный интеграл с одинаковыми пределами равен нулю: .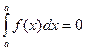

5. Отрезок интегрирования можно разбивать на части: .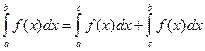

6. Формула Ньютона-Лейбница: Если F(x) – первообразная функция для непрерывной функции y=f(x), т.е. F'(x) = f(x), то имеет место формула: .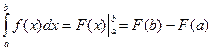

7. Замена переменных: 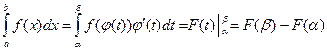, где .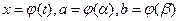

8. Интегрирование по частям: Если u=u(x), v=v(x) – функции, имеющие непрерывные производные на некотором промежутке, то справедлива формула интегрирования по частям: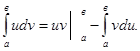

Геометрический смысл определённого интеграла

	Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [a; b] функции f(x), осью ОХ и прямыми х=а и х=в:
	Площадь криволинейной трапеции, ограниченной графиком непрерывной отрицательной на промежутке [a; b] функции f(x), осью ОХ и прямыми х=а и х=в:
	Если функция изменяет знак на промежутке [a; b], то
	Площадь фигуры, ограниченной двумя пересекающимися кривыми y=f(x) и y=g(x) таких, что f(x) g(x) для любого х , где а и b – абсциссы точек пересечения графиков функций: .
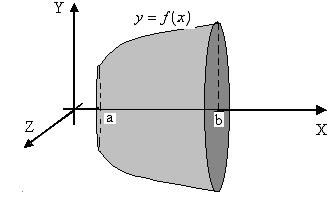
	Объём тела, полученного в результате вращения вокруг оси ОХ криволинейной трапеции, ограниченной графиком непрерывной и неотрицательной функции y=f(x) на отрезке [a; b]: