Решение. 1. Область определения функции это множество значений переменной x для которой определена функция

1. Область определения функции это множество значений переменной x для которой определена функция. В данном случае ограничения появляются из условия .

.

Функция непрерывна на своей области определения.

2. Функция не является периодической.

Проверим функцию на четность. Для этого должны выполняться условия:

- функция четная,

- функция нечетная.

Так как область определения не симметрично относительно нуля, то условие не выполнено и, следовательно, это функция общего вида.

3. Найдем точки пересечения с осями координат и промежутки знакопостоянства.

а) c осью 0x. . То есть это точка (0;0);

б) c осью 0y. . То есть это точка (0;0);

Промежутки знакопостоянства найдем методом интервалов.

Таким образом: .

4. Найдем промежутки монотонности функции и ее экстремумы. Для этого найдем производную функции, используя правило дифференцирования частного.

Функция возрастает на некотором промежутке, если ее производная на этом отрезке положительна и убывает, если производная отрицательна.

Таким образом, функция убывает на каждом из промежутков:

Функция возрастает на промежутке .

Точка x=-3 является точкой минимума, так как в ней производная равна нулю и при переходе через эту точку производная меняет знак с «+» на «-» .

Других экстремумов нет.

5. Наибольшего и наименьшего значения у функции нет, так как она не ограничена на области определения.

6. Найдем промежутки выпуклости и вогнутости функции. Для этого найдем вторую производную функции.

Функция выпукла вниз на промежутках и выпукла вверх на промежутке . Точка x=0 является точкой перегиба.

7. Найдем асимптоты.

Так как есть точка x=-1, которая не входи в область определения, то возможно, у функции будут вертикальные асимптоты.

, , следовательно прямя x=-1 является вертикальной асимптотой.

Исследуем функцию на наличие наклонных и горизонтальных асимптот.

, , следовательно горизонтальных асимптот нет.

Ищем асимптоту в виде y = kx + b.

, следовательно есть наклонные асимптоты.

.

Таким образом наклонная асимптота имеет вид , при .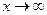

8. Множество значений функции .

9. График функции.