 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Примеры. 1.Найти площадь плоской фигуры, ограниченной графиком функции
|
|
1. Найти площадь плоской фигуры, ограниченной графиком функции
y = sin x и осью абсцисс при условии 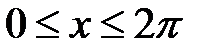 .
.
З а м е ч а н и е. Важный момент решения –построение чертежа!
Алгоритм построения чертежа:
1шаг. Построить все прямые;
2 шаг. Только потом строить графики других функций, выгоднее их строить точечно;
3 шаг. После того, как чертеж поострен, прикинуть, как найти пределы интегрирования: по чертежу или аналитически.
Решение:
1.Выполним чертеж
| x |
| 2p |
| 0 |
| y |
| p |
Рис.1.6.
Разобьём отрезок 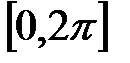 на два отрезка:
на два отрезка: 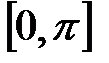 и
и 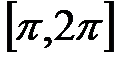 . На первом из них sin x
. На первом из них sin x 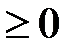 , на втором sin x
, на втором sin x 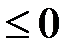 . Тогда, используя формулы, находим искомую площадь:
. Тогда, используя формулы, находим искомую площадь:
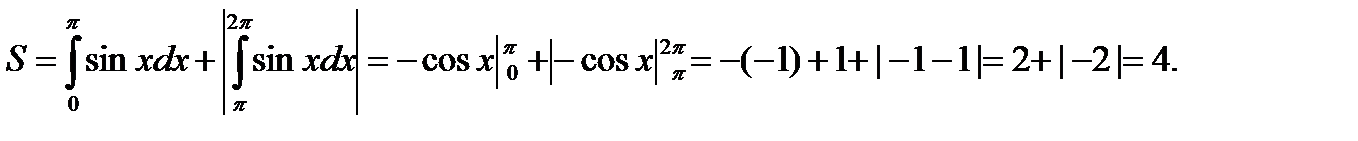
Ответ:4 
2. Вычислить площадь фигуры, ограниченной линиями 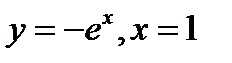 и координатными осями.
и координатными осями.
Решение: 1. Выполним чертеж:
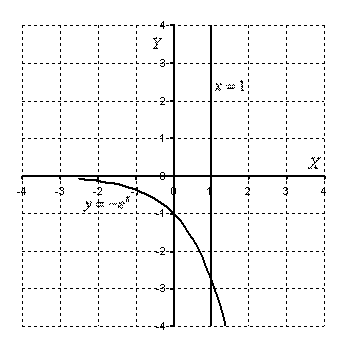
Рис.1.7.
Если криволинейная трапеция полностью расположена под осью OX, то ее площадь можно найти по формуле:
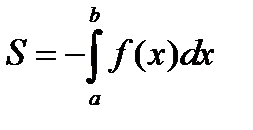
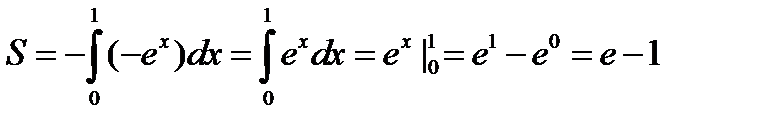
Ответ: 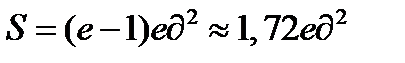
3. Найти площадь фигуры, ограниченной линиями 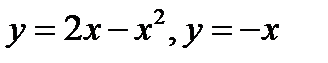
Решение:1. Построим чертеж
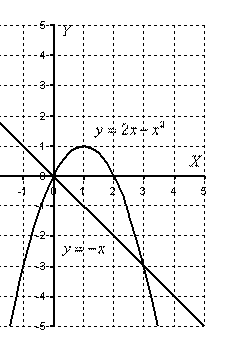
Рис.1.8.
Н а п о м и н а н и е: сначала строим прямую и только потом – параболу.
Определение: Если на отрезке 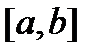 некоторая непрерывная функция f(x) больше либо равна некоторой непрерывной функции g(x), то площадь соответствующей фигуры можно найти по формуле:
некоторая непрерывная функция f(x) больше либо равна некоторой непрерывной функции g(x), то площадь соответствующей фигуры можно найти по формуле: 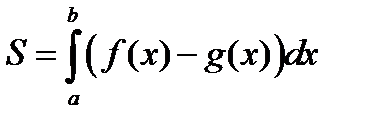
В нашем примере на отрезке [0,3] парабола располагается выше прямой, а поэтому из 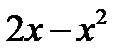 необходимо вычесть –x.
необходимо вычесть –x.
Воспользуемся формулой 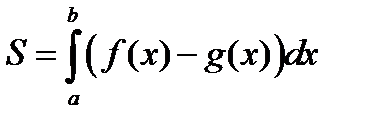 , откуда имеем:
, откуда имеем:
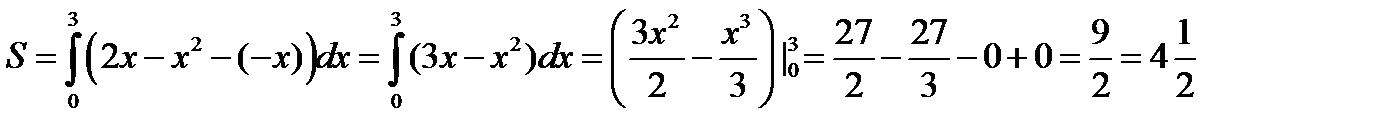
Ответ: 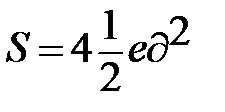 .
.
4. Вычислить площадь фигуры, ограниченной линиями
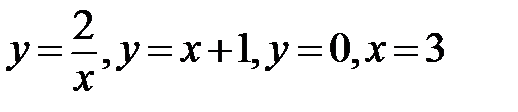
Решение:
1.Выполним чертеж.
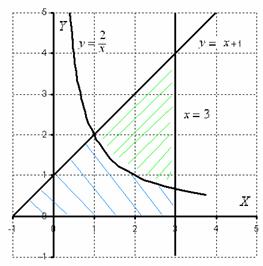
Рис.1.9.
Внимательно смотрим на условие - чем ограниченна фигура! На рисунке фигура заштрихована более крупно.
Наша фигура состоит из двух криволинейных трапеций:
1. На отрезке[-1,1] над осью OX расположен график 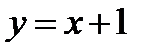 ;
;
2. На отрезке [1,3]над осью OX расположен график гиперболы 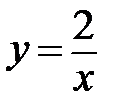 .
.
Поэтому площадь криволинейной трапеции состоит из двух площадей, поэтому:
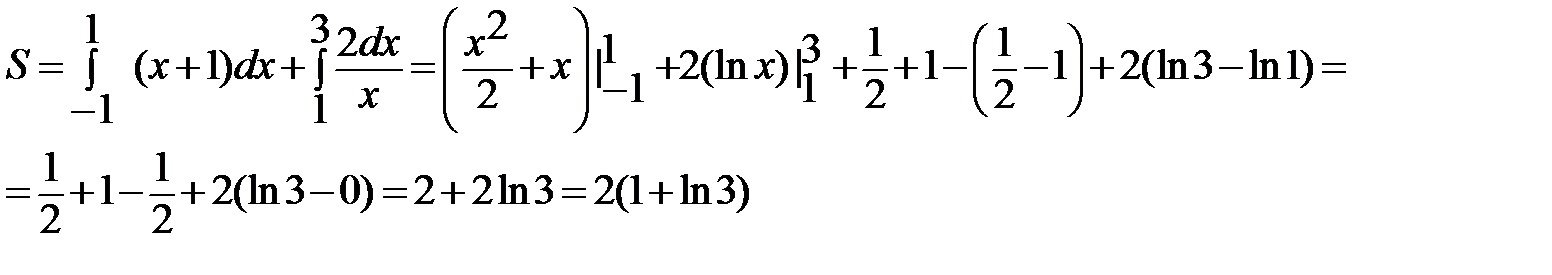
Ответ: 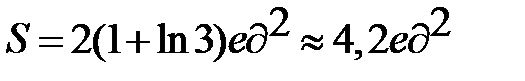 .
.
5. Вычислить площадь фигуры, ограниченной линиями

Решение:
Выразим в функциях y через x: 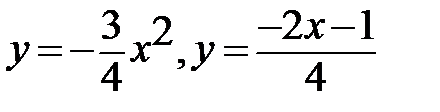
Построим чертеж

Рис.1.10.
На чертеже видно, что целым числом выражен только верхний предел, b=1, но нижний предел точно по чертежу определить сложно, поэтому определим его аналитически. Для этого решим уравнение:
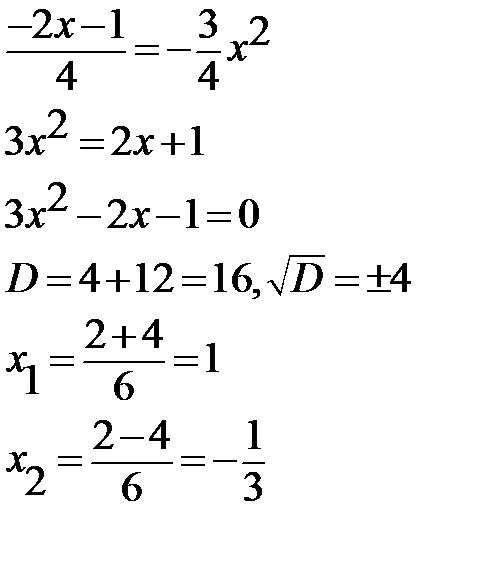
Рассмотрим отрезок 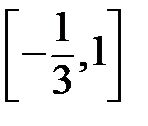 где,
где, 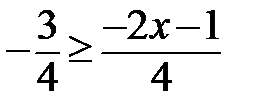
По формуле 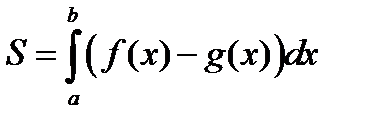 имеем:
имеем:
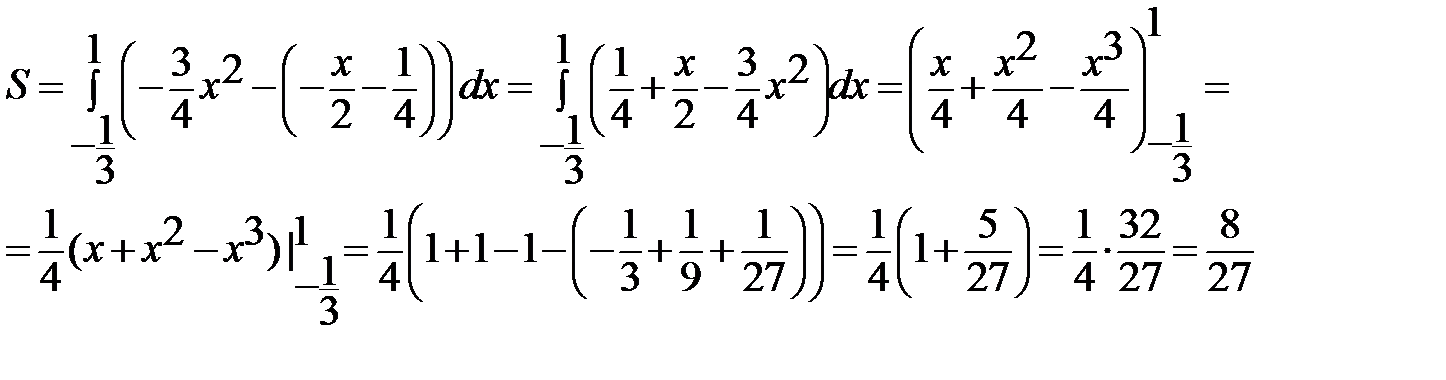
Ответ: 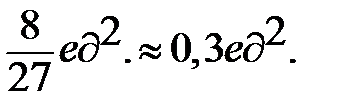
Дата публикования: 2014-11-03; Прочитано: 983 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
