Свойства определённого интеграла

1.

2. Постоянный множитель можно выносить за знак определённого интеграла:

3. Определённый интеграл от суммы двух функций равен сумме определённых интегралов от этих функций:

4. При перестановке пределов интегрирования определённый интеграл меняет знак на противоположный:

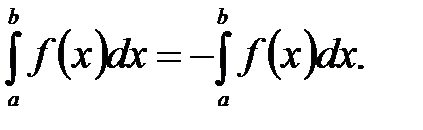
5. Интеграл по отрезку равен сумме интегралов по его частям:

где a<c<b.

6. Теорема об оценке интеграла

Если для 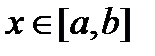, тогда значения интеграла от этой функции не менее произведения m на длину отрезка и не более произведения M на длину отрезка.

7. Теорема о среднем значении

Если f(x) непрерывна на отрезке , то существует такое значение , что f(x₀)=f_ср – среднее значение f на отрезке.