Вычисление объёмов

a

0

x

b

y

y=f(x)

Если тело образовано вращением вокруг оси Ох криволинейной трапеции, ограниченной непрерывной кривой y=f(x) (), осью Ох и прямыми x=a, x=b (a<b), то

или

Рис.7.

c

0

x

d

y

x=g(y)

Рис.8.

Вокруг Оу:

1

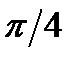
x

y

0

y=tg(x)

1. Найти объем тела, полученного вращением y=tgx вокруг оси Ox, .

Рис.1.9.

Решение: Как и при решении задач на нахождение площади, решение начинается с чертежа плоской фигуры. ТО есть на плоскости XOY необходимо построить фигуру, ограниченные линиями, далее используем формулу вычисления объема тела . Плоская фигура ограничена графиком функции , это и есть та функция, которая подразумевается в формуле.

.

Ответ:

В ответе всегда необходимо указывать размерность кубические единицы .

2. Вычислить объем тела, полученный при вращении вокруг оси абсцисс фигуры, ограниченный линиями

Решение:1 шаг. Изобразим чертеж

Рис. 1.10.

Внимательно изучаем условие и определяем, что искомая фигура представляет собой заштрихованную часть, отсюда следует, что объем тела вращения получаем как разность объемов тел.

Используем стандартную формулу вычисления объема тела вращения

2 шаг. Вычислим объем тела вращения, ограниченный сверху прямой

3 шаг. Вычислим объем тела вращения ограниченный сверху прямой

4 шаг. Найдем объем искомого тела вращения

Ответ: .

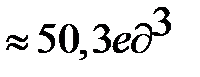3. Вычислить объем фигуры, ограниченный линиями , который получен вращением плоской фигуры вокруг оси OY.

Решение: 1 шаг. Построим чертеж, для этого выразим x через y, получим: ,

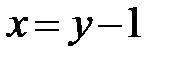
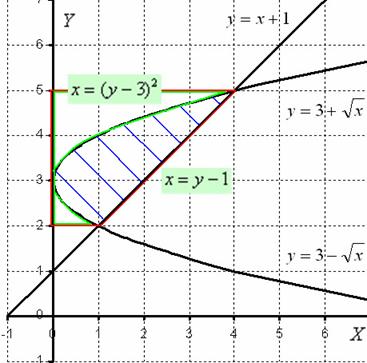
Рис. 1.11.

2 шаг. Посмотрим на ось OY, нужная нам фигура лежит на отрезке [2,5] и прямая 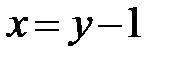лежит выше прямой , поэтому воспользуемся формулой

3 шаг. Рассмотрим на чертеже необходимую фигуру вращения и делаем вывод, что искомая фигура состоит из разности двух тел вращения, ограниченные функциям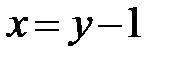и и

4 шаг. Найдем объем тела вращения

5 шаг. Найдем объем тела вращения

6 шаг. Найдем искомую фигуру тела вращения:

Ответ: