 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Сходится, а если предел не существует, то интеграл называют расходящимся
|
|
Геометрически для неотрицательной при 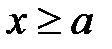 функции f(x) несобственный интеграл по аналогии с собственным интегралом представляет собой площадь фигуры, ограниченной сверху графиком функции y=f(x), слева отрезком прямой x=a и снизу осью Ox.
функции f(x) несобственный интеграл по аналогии с собственным интегралом представляет собой площадь фигуры, ограниченной сверху графиком функции y=f(x), слева отрезком прямой x=a и снизу осью Ox.
| a |
| 0 |
| x |
| y |
| y=f(x) |
Рис.10.
Что значит вычислить несобственный интеграл? Вычислить несобственный интеграл – это значит найти ЧИСЛО или доказать, что оно расходится. Несобственные интегралы бывают двух видов: несобственный интеграл с бесконечным пределом (амии) интегрирования и несобственные интегралы от неограниченных функций. Несобственный интеграл  существует только тогда, когда подынтегральная функция
существует только тогда, когда подынтегральная функция 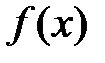 непрерывна на интервале
непрерывна на интервале 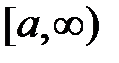 .
.
Несобственный интеграл  численно равен площади заштрихованной площади фигуры, при этом возможны два случая:
численно равен площади заштрихованной площади фигуры, при этом возможны два случая:
1)Если фигура бесконечна, то 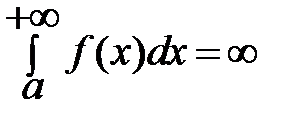 , тогда говорят, что несобственный интеграл расходится.
, тогда говорят, что несобственный интеграл расходится.
2)Если  , то несобственный интеграл сходится.
, то несобственный интеграл сходится.
Важно! Когда для решения предложен любой несобственный интеграл, то, вообще говоря, ни о какой площади речь не идет и чертеж строить не нужно. Главное найти ЧИСЛО или доказать, что несобственный интеграл расходится.
Примеры:
1. Исследовать на сходимость интегралы:
а) 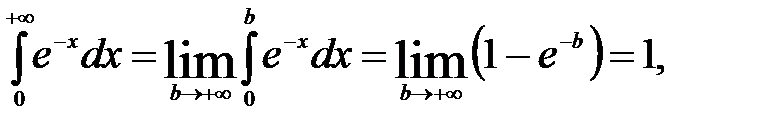 т.е. данный несобственный интеграл сходится.
т.е. данный несобственный интеграл сходится.
б) 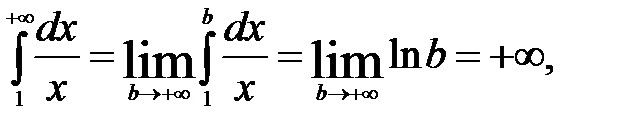 т.е. данный интеграл расходится.
т.е. данный интеграл расходится.
в) Установим, при каких значениях 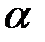 интеграл
интеграл 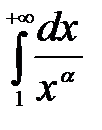 сходится.
сходится.
Случай 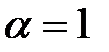 был рассмотрен в примере б). Если
был рассмотрен в примере б). Если 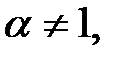 то
то
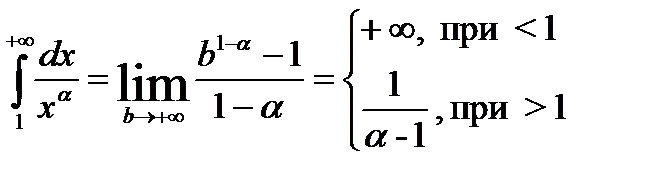 .
.
Значит, данный интеграл сходится при 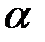 >1 и расходится при
>1 и расходится при 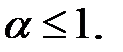
Аналогично определяются следующие несобственные интегралы

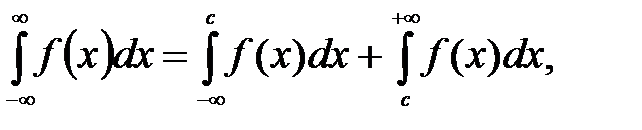
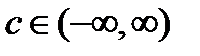
Дата публикования: 2014-11-03; Прочитано: 470 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
