Линейные уравнения

Дифференциальное уравнение называется линейным, если оно линейно (т.е. первой степени) относительно искомой функции y и ее производной 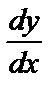. Общий вид линейного уравнения

y^|+P(x)y=Q(x). (6.4.6)

Линейное уравнение сводится к двум уравнениям с разделяющимися переменными, если искомую функцию y заменить произведением двух вспомогательных функций u и v, т.е. положить y=uv. Тогда

,

и данное уравнение (6.4.6.) примет вид

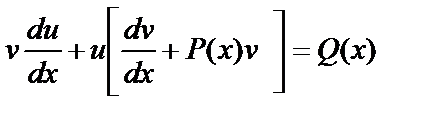. (6.4.7)

Пользуясь тем, что одну из вспомогательных функций, например v, можно выбрать произвольно, подберем ее так, чтобы выражение в квадратных скобках обратилось в нуль, т.е. в качестве v возьмем одно из частных решений v=v(x) уравнения с разделяющимися переменными

.

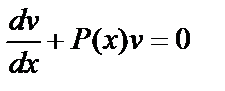Подставляя выражение v=v(x) в уравнение (6.4.7), получаем уравнение относительно функции u:

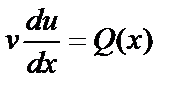, (6.4.8)

которое также является уравнением с разделяющимися переменными. Найдя общее решение уравнения (6.4.8) в виде u=u(x,C), получим общее решение линейного уравнения (6.4.6):

y=u(x,C)v(x).