Разложение в ряд Маклорена некоторых элементарных функций

I Разложение функции

Эта функция имеет производных всех порядков при любом х: (n=1,2,3,…)

Проверим выполнение условий теоремы 2:

если взять любой промежуток 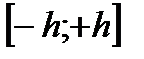, то в нем верна оценка

(т. е. для всех значений х модули всех производных ограничены одним и тем же числом ).

Поэтому по теореме 2 функция разлагается в сходящийся к ней ряд Маклорена в любом промежутке 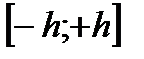, т. е. иначе говоря, при всех х (всюду).

Найдем коэффициенты ряда:

таким образом, при любых х верно разложение:

Пример 6.2.31. Разложить в ряд Маклорена функцию 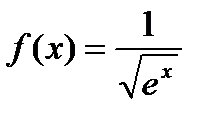; указать интервал сходимости

Решение ,

II Разложение функции

Она имеет производные всех порядков:

Очевидно, условия теоремы 2 выполняются: при всех х и n производная функции по модулю не превосходит единицы.

Следовательно, разлагается в ряд Маклорена и разложение справедливо при всех х.

Найдем коэффициенты ряда:

Таким образом, при любых х верно разложение:

(*) ,

В ряде присутствуют только нечетные степени х; это естественно, т. к. - нечетная функция.

Можно считать равенство (*) определением функции , т. к. радиус сходимости ряда равен бесконечности, и, следовательно, сумма ряда определена и непрерывна на всей числовой оси. Эту сумму и можно по определению считать функцией такое определение не связано с геометрическим построением, с которыми эта функция так тесно связана в школьном курсе математики.

III Разложение функции

Разложение в ряд этой функции можно получить так же, как и для

Но можно получить его путем дифференцирования разложения для :

,

Пример 6.2.32. Разложить функцию в ряд по степеням х.

Решение:

IV Разложение функции

Мы должны получить разложение логарифмической функции (в ряд Маклорена) по степеням х. Надо, чтобы сама функция и все ее производные имели смысл при х=0.

Если взять , , 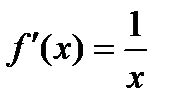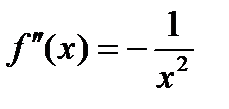и т. д.

Как видим, f(0) и f⁽ⁿ⁾(0) при всяком n лишены смысла. Поэтому рассматриваем функцию Эта функция и все ее производные определены при х=0.

Итак, ;

Разложим эту функцию в ряд, используя возможность почленного интегрирования степенных рядов.

Найдем ; производная может быть разложена в ряд Маклорена, т. к. дробь может рассматриваться как сумма геометрической прогрессии (убывающей) при 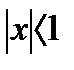(знаменатель прогрессии q=-x):

где (радиус сходимости ряда)

Проинтегрируем этот степенной ряд почленно в промежутк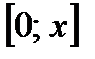е , где 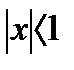(интервал интегрирования не выходит за пределы интервала сходимости ряда):

,

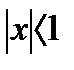
Сохраняется ли это равенство при х=±1?

При х=±1 теряет смысл функция , поэтому равенство при х=-1 лишено смысла.

При х=1 сохраняет смысл функция , она обращается в число Ряд сходится (по признаку Лейбница).

Остается проверить, имеет ли место равенство:

(*)

Из рассмотренных выше рассуждений справедливость равенства (*) пока еще не вытекает, т. к. доказали только, что разложение функции верно при 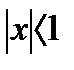.!Для проверки равенства (*) проведем оценку остаточного члена при х=1:

Закон образования производных найти легко:

Остаточный член (в форме Лагранжа):

найдем при х=1:

Т. к. , то при стремится к нулю: при . А это означает (теорема 1), что ряд (*) сходится и имеет своей суммой число , т. е. равенство (*) верно.

Итак, ,

V Разложение функции

; эту дробь при 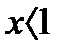можно рассматривать как сумму убывающей геометрической прогрессии со знаменателем :

Интегрируя в пределах от 0 до х, где 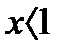, получаем: ; откуда имеем:

, (что будет показано ниже)

Проверим, не сохраняется ли это равенство и при х=±1.

При х=-1 – самостоятельно!

При х=1: ряд принимает вид:

который сходится (по теореме Лейбница).

!Остается проверить, имеет ли место равенство:

(*)

Для этого поступим следующим образом:

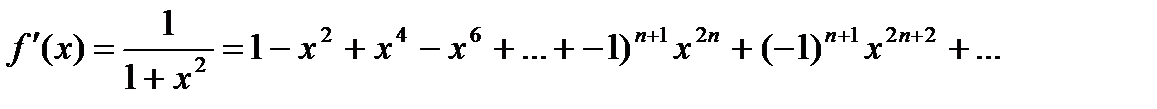т. е. приостанавливаемся на (n+1) члене!!!

Интегрируем это равенство (конечное число слагаемых) в промежутке от 0 до 1:

т.к. при , то, следовательно правая часть при (в силу равенства (**)): при ; это и означает, что сумма ряда (*) , т. е. равенство верно.