Дифференциальные уравнения высших порядков, допускающие понижение порядка

Уравнение вида

y⁽ⁿ⁾=f(x) (6.4.26)

решается последовательным n-кратным интегрированием. При каждом интегрировании получается одна произвольная постоянная, а в окончательном результате – n произвольных постоянных.

Уравнение второго порядка, не содержащее искомойфункции, т.е. уравнение вида

F(x,y^|,y^||)=0, (6.4.27)

при помощи подстановки y^|=p(x) (откуда 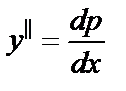) преобразуется в уравнение первого порядка

Уравнение второго порядка, не содержащее независимой переменной, т.е. уравнение вида

F(y,y^|,y^||)=0, (6.4.28)

при помощи подстановки y^|=p(y) (откуда ) сводится к уравнению первого порядка