 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Линейные однородные дифференциальные уравнения высших порядков с постоянными коэффициентами
|
|
Линейным однородным дифференциальным уравнением n-ого порядка с постоянными коэффициентами называется уравнение
y(n)+p1y(n-1)+p2y(n-2)+…+pn-1y|+pny=0, (6.4.29)
в котором все члены имеют первую степень относительно функции ее производных, а коэффициенты p1,p2,…,pn – постоянные.
Общее решение линейного однородного уравнения (6.4.29) имеет вид
y=C1y1+C2y2+…+Cnyn, (6.4.30)
где y1,y2,…yn – линейно независимые частные решения (фундаментальная система решений) этого уравнения, а C1,C2,…Cn – произвольные постоянные.
Для отыскания общего решения уравнения (6.4.29) составляется характеристическое уравнение
rn+p1rn-1+p2rn-2+…+pn-1r+pn=0, (6.4.31)
которое получается из уравнения (6.4.29) заменой в нем производных искомой функции соответствующими степенями r, причем сама функция заменяется единицей.
Тогда общее решение уравнения (6.4.29) строится в зависимости от характера корней уравнения (6.4.31):
1) каждому действительному однократному (т.е. простому) корню r в общем решении соответствует слагаемое вида Cerx;
2) каждому действительному корню r кратности k в общем решении соответствует слагаемое вида (C1+C2x+…+Ck-1xk-1)erx;
3) каждой паре комплексных сопряженных однократных корней 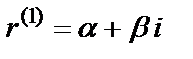 и
и 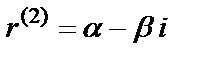 в общем решении соответствует слагаемое вида
в общем решении соответствует слагаемое вида 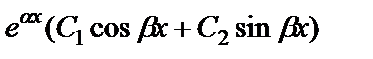 ;
;
4) каждой паре комплексных сопряженных корней 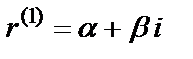 и
и 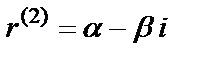 кратности L в общем решении соответствует слагаемое вида
кратности L в общем решении соответствует слагаемое вида
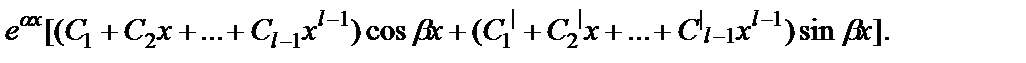
Дата публикования: 2014-11-03; Прочитано: 356 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
