Комплексные числа. Число , где и - действительные числа, а

КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ

Число , где и - действительные числа, а - так называемая мнимая единица, называется комплексным числом. Действительные числа и называются соответственно действительной и мнимой частями комплексного числа 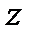и обозначаются: - есть действительное число; если , а , то число называется числом мнимым.

Два комплексных числа и считаются равными, если равны их действительные и мнимые части, т. е. = 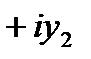при и

Будем изображать комплексное число с помощью точки на плоскости, абсцисса которой равна , а ордината . Тогда всякое комплексное число изобразится с помощью определенной точки, так называемой комплексной плоскости.

Положение точки, изображающей комплексное число z, можно определить также с помощью полярных координат r и φ будем называть соответственно модулем и аргументом комплексного числа z: r =|z|; φ = Arg z. Из определения модуля и аргумента следует, что если , то x = r cos φ =|z | cos (Arg z); y =r sinφ=|z| sin(Arg z);

tgφ (при х ).

Заметим, что величина j=Arg z имеет бесчисленное множество значений, отличающихся одно от другого на целое, кратное 2p. Если величину одного из углов обозначить через j₀, то совокупность величин всех углов запишется выражением

Arg z=j₀+2pk (k=0,±1, ±2,…).

Значение j=Arg z, принадлежащее промежутку ]- p,p[, назы­вается главным и обозначается j₀=arg z, т.е -p<arg z£p.

Следовательно,

Arg z= Arg z++2pk (k=0,±1, ±2,…).

Зная действительную х и мнимую у части комплексного числа z и пользуясь тем, что tg (arg z)=y/x, можно вычис­лить arg z по формуле

Числу 0 не приписывается какое - либо значение аргумента.

Всякое комплексное число, отличное от нуля, можно представить ь в тригонометрической форме

z=x+iy=rcosj+irsinj=r(cosj+isinj).

Замечание 1.1. С помощью формулы Эйлера e^ij=cosj+isinj можно представить комплексное число в показательной форме:

z= r e ^ij .

Комплексные числа z=x+iy и называют взаимно-сопряженными. При этом .

Сложение, вычитание и умножение комплексных чисел производят по правилам сложения, вычитания и умножения алгебраических многочленов, полагая при этом i²=-1, i³=-i, i⁴=1,…

При сложении и вычитании комплексных чисел отдельно склады­ваются и вычитаются их действительные и мнимые части:

(x₁+iy₁)±(x₂+iy₂)=(x₁+x₂)+i(y₁+y₂).

Умножение:

(x₁+iy₁) (x₂+iy₂)=(x₁x₂-y₁y₂)+i(x₁y₂+x₂y₁).

Деление определяется как действие, обратное умножению.

Деление удобно производить следующим образом; сначала умножить делимое и делитель на число, сопряженное делителю, после чего делитель станет действительным числом , а затем произвести деление действительной и мнимой частей отдельно;

Если воспользоваться тригонометрической формой записи чисел

z₁=r₁(cosj₁+isinj₁); z₂=r₂(cosj₂+isinj₂);

получим

z₁ z₂=r₁ r₂ [(cos(j₁+j₂)+isin(j₁+j₂)], (6.3.1)

т.e, при умножении комплексных чисел их модули перемножаются, а аргументы складываются:

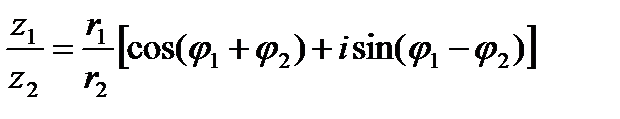. (6.3.2)

Из правила умножения следует правило возведения в целую положительную степень: если

z=r(cosj+isinj), то zⁿ=rⁿ(cosnj+isin nj). (6.3.3)

Нетрудно убедиться, что формула справедлива и при целом отрицательном n.

Извлечь корень целой положительной степени n из числа z - значит найти такое число , n-я степень которого равна z.