Дифференциальные уравнения. Определение 6. 4. 1. Уравнение, связывающее независимую переменную, неизвестную функцию и ее производные или дифференциалы различных порядков

Основные понятия

Определение 6.4.1.Уравнение, связывающее независимую переменную, неизвестную функцию и ее производные или дифференциалы различных порядков, называется обыкновенным дифференциальным уравнением.

Определение 6.4.2. Порядком дифференциального уравнения называется порядок старшей производной, входящей в данное уравнение.

Например, уравнение - первого порядка; - второго порядка; 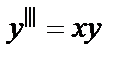- третьего порядка и т. д.

Решением дифференциального уравнения называется функция y=y(x), удовлетворяющая этому уравнению. График решения на плоскости xOy называется интегралом уравнения.

Процесс нахождения решения называется интегрированием дифференциального уравнения.

Если решение уравнения получено в неявном виде , то оно обычно называется интегралом уравнения.

Задача Коши для уравнения

(6.4.1)

ставится следующим образом. Среди всех решений уравнения (6.4.1) требуется найти решение y=y(x), для которого функция y(x) вместе со своими производными до (n-1)-го порядка включительно принимает заданные значения при заданном значении x₀ аргумента x, т.е.

(6.4.2)

где x₀, y₀, y₀^|,…,y₀^(n-1) – заданные числа.

Условия (6.4.2) называются начальными условиями решения y=y(x), а само это решение – частным решением уравнения (6.4.1), удовлетворяющим начальным условиям (6.4.2).

Общее решение уравнения (6.4.1) – это решение вида 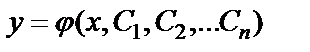, зависящее от n произвольных постоянных C₁, C₂, …C_n, которые можно подобрать таким образом, чтобы удовлетворить любой системе начальных условий.

Частное решение уравнения (6.4.1) может быть получено из общего решения при некоторых числовых значениях произвольных постоянных C₁, C₂, …C_n.