Уравнения Лагранжа и Клеро

Уравнение Лагранжа. Уравнением Лагранжа называется уравнение вида

, (6.4.16)

т.е. линейное относительно x и y с коэффициентами, зависящими от y^|, причем коэффициент при x не равен y^|.

Для интегрирования уравнения Лагранжа воспользуемся параметрическим методом. Полагая y^|=p, перепишем уравнение (6.4.16) в виде

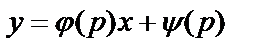. (6.4.17)

Дифференцируя по x, имеем

,

откуда после замены y^| на p, умножения на и соответствующих алгебраических преобразований [в частности, деления обеих частей уравнения на ] получим

. (6.4.18)

Это уравнение является линейным относительно функции x и производной 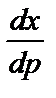. Его общее решение имеет вид

x=F(p,C). (6.4.19)

Подставляя найденное для x выражение в соотношение (6.4.16), получим

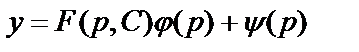. (6.4.20)

Соотношения (6.4.19) и (6.4.20) дают общее решение уравнения Лагранжа в параметрической форме:

Заметим, что если уравнение =0 имеет действительные корни, то подставляя эти корни в уравнение (6.4.17), мы также получим решения уравнения Лагранжа, которые могут оказаться как ч а с т н ы м и, так и о с о б ы м и. (Решение, в каждой точке которого нарушается единственность решения задачи Коши, называется особым решением.)

Уравнение Клеро. Уравнением Клеро называется уравнение вида

, (6.4.21)

т.е. частный случай уравнения Лагранжа, когда .

Положим y^|=p, тогда

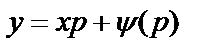. (6.4.22)

Дифференцируя по x, имеем

Последнее уравнение распадается на два:

(6.4.23)

Из уравнения следует, что p=C. Подставляя это выражение в равенство (6.4.21), получим общее решение уравнения Клеро:

(6.4.24)

Формально общее решение получается из уравнения (6.4.21) заменой y^| на C.

Уравнение Клеро имеет особое решение, получающееся в результате исключения параметра C из системы уравнений

(6.4.25)