 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Цилиндрические поверхности
|
|
Цилиндрическая поверхность второго порядка задается в некоторой надлежаще выбранной для данной поверхности канонической системе координат уравнением:
F(x,y)=0 (7.2.1.)
Кривая, определяемая уравнением (7.2.1.) в плоскости Oxy, является направляющей кривой цилиндрической поверхности. Эта кривая может быть эллипсом, действительным или мнимым, гиперболой или параболой, в зависимости от чего мы и различаем эллиптические (рис. 7.1.), мнимые эллиптические, гиперболические (рис. 7.2.) и параболические (рис. 7.3.) цилиндры, канонические уравнения которых совпадают с каноническими уравнениями направляющих кривых.
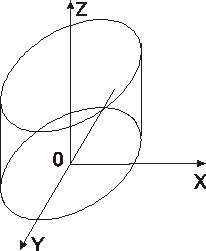
рис.7.1. Эллиптический цилиндр. Каноническое уравнение 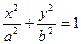

рис.7.2. Гиперболический цилиндр. Каноническое уравнение 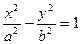 .
.
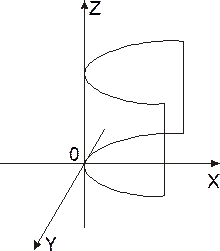
рис.7.3. Параболический цилиндр. Каноническое уравнение x2=2pZ.
Замечание. Если направляющая (7.2.1) есть пара прямых, то цилиндрическая поверхность выражается в пару плоскостей (пересекающихся, параллельных или совпадающих, действительных или мнимых -
в зависимости от соответствующего свойства лежащей в основании пары прямых).
Дата публикования: 2014-11-04; Прочитано: 489 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
