Ряд Маклорена

Если функция определена и 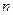раз дифференцируема в окрестности точки , то она может быть разложена в степенной ряд: (14.3)

Выразим коэффициенты ряда через 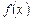. Для этого найдем производные функции : ; ; ;

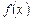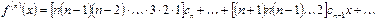
Полагая , получим: . Откуда имеем: Подставляя значения этих коэффициентов в (14.3), получим разложение функции 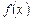в ряд Маклорена:

, (14.4)

где .

Так же как и для числовых рядов сумму 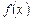ряда Маклорена можно представить в виде ,

где - n-я частичная сумма ряда, 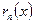- -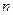й остаток ряда.

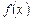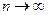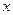Теорема. а) Для того, чтобы ряд Маклорена сходился к функции , необходимо и достаточно, чтобы при остаток ряда стремился к нулю, т.е. для всех значений из интервала .

б) Если функция 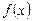разложена в ряд Маклорена, то это разложение единственное.

Имеем ; ; Область сходимости ряда .

49. Разложение в ряд Маклорена функции y =ln (1+x) (вывод). Интервал сходимости полученного ряда.

Рассмотрим

А теперь заметим, что функция является суммой ряда 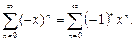Теперь воспользуемся теоремой о почленном интегрировании степенного ряда:

Область сходимости ряда .

50. Разложение в ряд Маклорена функции у= (1+ х) ⁿ (вывод). Интервал сходимости полученного ряда.

, где 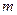- любое действительное число.

Имеем: ,

,

,

,

…,

.

При : ,

,

,

,

…,

По формуле 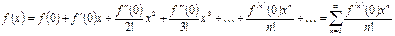(ряд Маклорена):

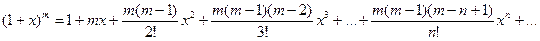. (1.1)

Интервал сходимости ряда (на концах интервала при сходимость ряда зависит от конкретных значений ).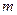

Ряд (1.1) называется биномиальным. Если 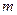- целое положительное число, то биномиальный ряд представляет формулу бинома Ньютона, т.к. при , член ряда и все последующие равны нулю, т.е. ряд обрывается, и вместо бесконечного разложения получается конечная сумма.