Линейные дифференциальные уравнения 1-го порядка

Дифференциальные уравнения 1-го называется линейным, если оно имеет вид

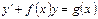, (12.7)

где и - некоторые непрерывные функции переменной .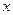

Если уравнение (12.7) называется однородным, в противном случае – неоднородным.

Решение. а) Если , то однородное уравнение является уравнением с разделяющимися переменными.

б) Если , то для неоднородного уравнения сделаем замену , тогда , и уравнение (12.7) сводится к виду: , или .

Пусть выражение, стоящее в скобках равно нулю, тогда имеем два уравнения с разделяющимися переменными:

Решая сначала первое уравнение из системы, находим какое-либо частное решение , которое подставляем во второе уравнение системы и находим .

Окончательно, имеем решение: .

Пример. Решить уравнение .

Решение. Разделив на 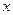исходное уравнение, получим линейное уравнение .

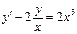Положим , тогда . .

Найдем частное решение первого уравнения системы (пусть ) .

Рассмотрим второе уравнение из системы:

Таким образом, общее решение дифференциального уравнения .