Расходимость гармонического ряда

Рассмотрим ряд: , который носит название гармонического ряда.

Для гармонического ряда необходимый признак сходимости выполнен: .

Однако это не означает, что ряд сходится.

Покажем это. Рассмотрим частичные суммы ряда и :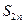

Найдем разность :

.

Заменяя в сумме каждое слагаемое наименьшим , придем к вспомогательному неравенству:

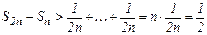или .

Если бы гармонический ряд сходился, тогда , а мы имеем . Это значит, что гармонический ряд расходится.

Таким образом, если общий член ряда стремится к нулю, то еще нельзя сделать вывод о сходимости ряда. Необходимо дополнительное исследование с помощью достаточных признаков сходимости ряда.