Определение числового ряда. Сходимость числового ряда. Необходимый признак сходимости рядов (доказать). Примеры

При решении ряда математических задач, например в приложениях математики в экономике, приходится рассматривать суммы, составленные из бесконечного множества слагаемых. Эта проблема решается в теории рядов.

Понятие числового ряда. Сходимость ряда и его сумма

Определение. Числовым рядом называется бесконечная последовательность чисел соединенных знаком сложения: , (13.1)

где 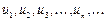называются членами ряда, а 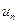- общим или 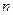-м членом ряда, - натуральные числа.

Ряд (13.1) считается заданным, если известен его общий член .

Например, дан ряд общий член: .

Более сложной является задача: по нескольким членам написать общий член.

Пример. Найти общий член ряда . Решение. Нетрудно убедиться, что .

Определение. Сумма первых 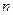членов ряда называется 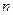-й частичной суммой ряда.

Определение. Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е.

. (13.2)

Число называется суммой ряда, поэтому можно записать: . (13.3)

Определение. Если конечного предела последовательности частных сумм не существует, то ряд называется расходящимся.

Пример. Исследовать сходимость геометрического ряда (составленного из членов геометрической прогрессии): .

Решение. Требуется установить, при каких значениях знаменателя прогрессии ряд сходится, а при каких – расходится. Из школьного курса алгебры известно, что . Рассмотрим возможные варианты.

1) Если , то , , т.е. - ряд сходится.

2) Если , то , следовательно, и ряд расходится.

3) Если 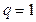, то ряд примет вид , , , т.е. ряд расходится.

4) Если , то ряд примет вид , при 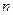- четном, при 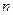- нечетном, не существует и ряд расходится.

Таким образом, геометрический ряд сходится к сумме при и расходится при .