 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Рассмотрим некоторые типы дифференциальных уравнений 1-го порядка
|
|
1) Неполные дифференциальные уравнения 1-порядка.
Дифференциальное уравнение 1-го порядка (12.3) называется неполным, если оно не содержит в явном виде искомой функции 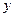 или независимой переменной
или независимой переменной 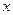 :
:
1. 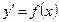 (не содержит
(не содержит 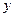 ) (12.4.1)
) (12.4.1)
Решение: 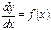 ,
, 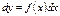 , откуда
, откуда 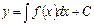 .
.
2. 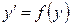 (не содержит
(не содержит 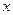 ) (12.4.2)
) (12.4.2)
Решение: Удобно искать в виде 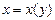 . т.к.
. т.к.  , то ур-е можно записать:
, то ур-е можно записать: 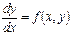
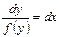 , откуда
, откуда 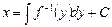 .
.
Пример. а) 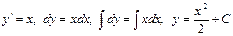 .
.
б) 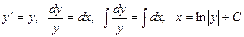 ,
, 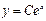 .
.
2) Дифференциальные уравнения 1-го порядка с разделяющимися переменными.
Дифференциальное уравнение 1-го порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде:
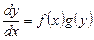 , (12.5.1)
, (12.5.1)
или в виде 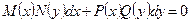 . (12.5.2)
. (12.5.2)
где 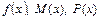 - некоторые функции переменной
- некоторые функции переменной 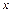 ;
; 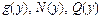 - функции переменной
- функции переменной 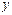 .
.
Для нахождения решения (12.5.1) и (12.5.2) преобразовывают таким образом, чтобы функции, зависящие от 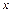 и
и  были в одной части равенства, а функции, зависящие от
были в одной части равенства, а функции, зависящие от 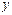 и
и 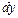 в другой. Затем интегрируем обе части равенства.
в другой. Затем интегрируем обе части равенства.
(12.5.1)Решение: 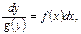 или или 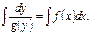
| (12.4.2) 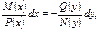 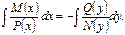
|
Пример. Решить уравнение 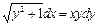 .
.
Решение. Разделяя переменные, имеем 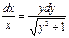 . Проинтегрируем левую и правую часть равенства
. Проинтегрируем левую и правую часть равенства 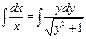 . Далее имеем
. Далее имеем 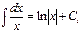 .
.
 , Окончательно имеем
, Окончательно имеем 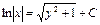 .
.
Уравнения вида 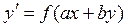 , где
, где 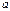 и
и 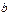 - некоторые числа, приводятся к уравниваниям с разделяющимися переменными заменой
- некоторые числа, приводятся к уравниваниям с разделяющимися переменными заменой 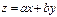 (или
(или 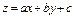 , где
, где 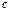 - некоторое число).
- некоторое число).
Пример. Решить уравнение 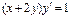 .
.
Решение: Пусть 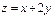 , тогда
, тогда 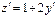 , откуда
, откуда 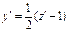 , или
, или 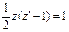 . Выразим
. Выразим  :
: 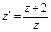 , и
, и 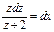 .
.
Интегрируем: 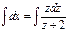 , или
, или 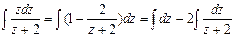 , следовательно
, следовательно 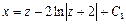 .
.
Возвращаемся к первоначальным переменным: 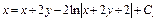 или
или 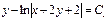 , где
, где 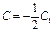 .
.
Дата публикования: 2014-11-04; Прочитано: 418 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
