Понятие о дифференциальном уравнении. Общее и частное решения. Задача Коши. Задача о построении математической модели демографического процесса

Определение. Дифференциальным уравнением называется уравнение, связывающее искомую функцию одной или нескольких переменных, эти переменные и производные различных порядков искомой функции.

Определение. Если искомая функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным, если от нескольких переменных – то уравнением в частных производных.

Рассмотрим пример. Найти первообразную , если .

Решение. Раньше мы эту задачу решали с помощью неопределенного интеграла. Однако, ее можно рассматривать как задачу о нахождении функции , удовлетворяющей уравнению . .

В общем случае дифференциальное уравнение можно записать в виде:

. (12.1)

Например: .

Определение. Дифференциальное уравнение 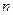-го порядка называется разрешенным относительно старшей производной, если оно имеет вид:

, (12.2)

где - некоторая функция от переменной.

Определение. Решением дифференциального уравнения (12.1) называется такая функция , которая при подстановке ее в это уравнение обращает его в тождество.

Например, есть решение уравнения , т.к. .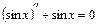

Определение. Задача о нахождении решения некоторого дифференциального уравнения называется задачей интегрирования этого дифференциального уравнения. График решения дифференциального уравнения называется интегральной кривой.

Пример. Решить уравнение: .

Решение. Поскольку , то . Интегрируя левую и правую часть равенства, получим . Т.к. , то разделив переменные имеем . Интегрируя вторично, получим решение: , .

Проверка: .

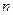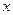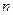Определение. Общим решением дифференциального уравнения (12.1) –го порядка называется такое его решение , которое является функцией переменных и произвольных постоянных .

Определение. Частным решением дифференциального уравнения называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных .

Например, для уравнения 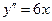, где .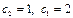

Задача о построении математической модели демографического процесса. Задача Коши

Задача. Из статистических данных известно, что для некоторого региона число новорожденных и умерших пропорционально текущей численности населения с коэффициентами пропорциональности и соответственно. Описать протекание демографического процесса во времени (найти закон изменения численности населения с течением времени).

Решение. Пусть 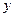- текущая численность населения . За время имеем 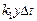родившихся и умерших, тогда прирост населения за есть:

, или , где .

Переходя к пределу при , получим ,

- дифференциальное уравнение демографического процесса.

Решая это уравнение, получим: .

Постоянная интегрирования есть численность населения при , т.е. .

Окончательно, имеем .

Определение. Задачей Коши называется задача, в которой для дифференциального уравнения заданы только начальные условия ( и т.д.) и не накладывается никаких граничных условий, (т.е. граница отсутствует).

Пояснение. Для полного описания эволюции какого-либо процесса помимо дифференциального уравнения необходимо, во-первых, задать картину процесса в некоторый фиксированный момент времени (начальные условия и т.д.) и, во-вторых, задать режим на границе области, где протекает процесс (граничные условия).