 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Признаки сравнения для знакоположительных рядов
|
|
Теорема 1(признак сравнения):
Если даны 2 ряда: 1) 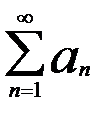 ,
,  ; 2)
; 2)  ,
, 
 n= 1, 2,…
n= 1, 2,…
для которых 
 , то 1ый ряд наз-сяможарируемым, а 2ой – можарантным.
, то 1ый ряд наз-сяможарируемым, а 2ой – можарантным.
Если 2ой ряд сход-ся, то сход-ся и 1й ряд. Если 1 ряд расх-ся, то расх-ся и 2ой ряд.
Теорема 2 (признак сравнения в предельной форме):
Если даны 2 ряда: 1) 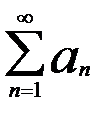 ,
,  ; 2)
; 2)  ,
, 
 n= 1, 2,…
n= 1, 2,…
И 
 , то
, то
1) Если сущ-т предел  (С≠0, С≠∞), то оба ряда либо одновременно сход-ся, либо одновременно расх-ся.
(С≠0, С≠∞), то оба ряда либо одновременно сход-ся, либо одновременно расх-ся.
2) Если  , то из сход-тиможарантного ряда следует сход-тьможарируемого ряда.
, то из сход-тиможарантного ряда следует сход-тьможарируемого ряда.
3) Если  , то из расх-тиможарантного ряда следует расх-тьможарируемого ряда.
, то из расх-тиможарантного ряда следует расх-тьможарируемого ряда.
Замечание: теорема 1 и 2 на практике не всегда удобны, т.к. для исследования сход-ти 1го из рядов необходимо знать поведение другого ряда или подбирать такой ряд, поведение которого известно.
Пример1: исследовать на сходимость ряд 
Сравним его с гармоническим рядом 
 >
> 
Гармонический ряд расх-ся, поэтому расх-ся и данный ряд по 1му признаку сравнения.
Пример2: исследовать сход-ть ряда  Для сравнения возьмём обобщенный гармонический ряд
Для сравнения возьмём обобщенный гармонический ряд  , кот-й сх-ся при α>1 и расх-ся при α≤1.
, кот-й сх-ся при α>1 и расх-ся при α≤1. 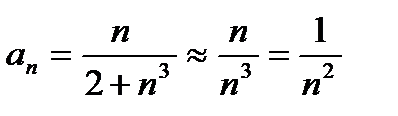 . Ряд
. Ряд  сх-ся. Положим
сх-ся. Положим  . Применяем 2ой признак сравнения:
. Применяем 2ой признак сравнения: 
Мы сравнивали данный ряд со сх-ся рядом. По второму признаку сравнения данный ряд сх-ся.
Дата публикования: 2014-11-04; Прочитано: 353 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
