 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
ДУ с разделяющимися переменными. Пример
|
|
Уравнения вида y’ =f1(x)f2(y) называются уравнениями с разделяющимися переменными. Метод их решения состоит в нахождении множителя для преобразования в уравнение с разделенными переменными. Это: dx/f2(y), тогда уравнения запишутся так: dy/f2(y)=f1(x)dx. Проинтегрируем ∫dy/f2(y)=∫f1(x)dx. После получения общего решения необходимо проверить, являются ли нули функции f2(y) решениями заданного уравнения и заключены ли они в общем интеграле.
Пример 1
Решить дифференциальное уравнение. 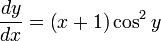
Разделим переменные: 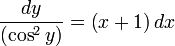
Т. к. начальные условия не заданы, возьмем неопределенный интеграл от обеих частей уравнения: 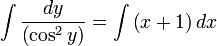
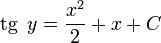
Осталось лишь выразить у через х: 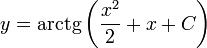
Найдем также нулевые решения: 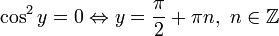
Дата публикования: 2014-11-04; Прочитано: 336 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
