Знакопеременные и знакочередующиеся ряды. Понятие абсолютной и условной сходимости. Знакочередующиеся ряды Лейбницевского типа

Знакопеременный ряд – ряд, содержащий как положительные так и отрицательные члены. Знакопеременный ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков .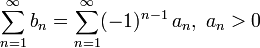

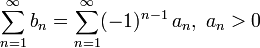Если ряд, состоящий из абсолютных величин, сходится, то знакочередующийся ряд сходится абсолютно. . В случае, если ряд сходится при отсутствии абсолютной сходимости, то он называется условно сходящимся.

Знакочер-ся ряды называются рядами л.типа, если они удовлетворены двум условиям:

1) .

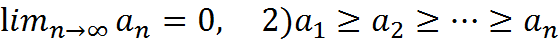Примеры:

40.Интегральный признак Коши для знакоположительных рядов. Пример исследования сходимости обобщенного гармонического ряда

Пусть члены ряда положительны и убывают, т.е. и пусть f(x)непрерывная, положительная убывающая функция, определённая для х>=1 и такая, что f(1)= 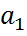, f(2)= ,…,f(n)= ,…,тогда и ряд сходятся или расходятся одновременно.

Исследуем вопрос о сходимости ряда . Решение. Применим интегральный признак сходимости, тогда Эта функция удовлетворяет всем условиям теоремы. Рассмотрим несобственный интеграл

1.Если , то =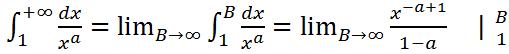

2. Если .

Ряд расходится. Тогда несобственный интеграл

поэтому и ряд, который является обобщенным гармоническим