Метод вариации произвольной постоянной

y’’ + py’ + qy = f(x) (1)

Для решения (1) Ла Гранже и был предложен универсальный метод. суть: он предложил искать решение неоднородного ур-я в том же виде что и решение соотв. однородного ур-я, пологая только что С₁ и С₂ – не константы, а ф-ии завис. от х. т.к y_оо=c₁y₁+c₂y₂,то структура y_он=с₁(x)y₁+с₂(x)y₂

фактически для нахождения y_он необходимо найти y₁ и y₂ из решения соотв. однородного ДУ, а затем определить ф-ии с₁(x) и с₂(x)… y₁ и y₂ ищем с помощью соотв. Характерестич. Ур-я. Для нахождения с₁(x) и с₂(x) учтем, что y_он – решение(1) Значит будучи подставленным в него, обращает (1) в тождество.

y’_он=(с₁(x)y₁+с₂(x)y₂)’=(с₁(x)y₁)’+(с₂(x)y₂)’=с₁’(x)y₁+с₁(x)y₁’+с₂’(x)y₂+с₂(x)y₂’ т.к вместо С₁ и C₂(констант) стали рассматрив. Ф-ии с₁(x) и с₂(x) то появилась лишняя степень, которой свободно можем распоряжаться: полагаем что с₁’(x)y₁+ с₂’(x)y₂=0 оставшееся выражение y’_он=с₁(x)y₁’+с₂(x)y₂’ диф. еще раз.

y’’_он= с₁’(x)y₁’+с₁(x)y₁’’+с₂’(x)y₂’+с₂(x)y₂’’ подставляем получ выражение в исходное ДУ

с₁’(x)y₁’+с₁(x)y₁’’+с₂’(x)y₂’+с₂(x)y₂’’+p(с₁(x)y₁’+с₂(x)y₂’)+q(с₁(x)y₁+с₂(x)y₂)=f(x)

раскрываем скобки и перегруппируем слагаемые с₁(x)(y₁’’+py₁’+qy₁)+c₂(x)(y₂’’+py₂’+qy₂)+с₁’(x)y₁’+с₂’(x)y₂’=f(x)

1-ая скобка обращается в 0 т.к по формуле y_оо=c₁y₁+c₂y₂ , y₁ и y₂ – линейное независимое решение соотв. однор. ур-я. Т.О для нахождения неизвестных ф-ий с₁(x) и с₂(x) необходимо решить систем ДУ

с₁’(x)y₁’+с₂’(x)y₂’=f(x)

с₁’(x)y₁+ с₂’(x)y₂=0

11.Двукратное интегрирование по частям на примере

В интегралах вида применяется двукратное интегрирование по частям, где u и dv могут быть выбраны произвольным образом, но при повторном интегрировании, также как при первом.

Точно также .

Пример:

А

Двукратное интегрирование по частям в данном интеграле с постоянным выбором u и v привёл нас в итоге к исходному интегралу, перенося кот. из прав. части в левую и приводя подобные, находим ответ.

12.Интегралы от функций, содержащих квадратный трехчлен . Примеры.

Интегралы вида 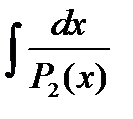, берутся с помощью замены переменной, предварительно выделив в многочлене полный квадрат.

Пр:

Для нахождения интеграла типа необходимо выполнить следующий алгоритм:

1)находим производную квадратного трёхчлена, стоящего в знаменателе, т.е.

2)формируем эту производную в числителе под интегральной ф-цией

3)разбиваем полученный интеграл на 2 вида

Второй интеграл типа 1, а первый интеграл берётся поднесением под знак дифф-ла

Пр:

35. Понятие ряда. Классификация рядов. Примеры .

Ряд- a₁+a₂+…+a_n+… (1), где в зависимости от стр-ры общего члена ряда an ф-ла (1) может описывать как числовой ряд, если a_n задается числовой формулой или (1) – функциональный ряд, если a_n задается функцией.

Классификация рядов:

1. числовые и функциональные:

· числовые: a₁+a₂+…+a_n+…

· функциональные:

2. расходящиеся и сходящиеся

3. Числовые ряды делятся на знакопостоянные и знакопеременные (знакочередующиеся)

Также приведем некоторые примеры числовых рядов, имеющих важное практическое значение:

1. 0+0+…+0+…= = 0 – ряд сходится

2. = -1+1-1+1-1… - знакочередующийся

S_n=

= ряд расходится

3. 1 + ½ + 1/3 + 1/4 + … +1/n+… = - гармонический ряд, расходящийся

4. Примером ряда может служить сумма бесконечная геометрическая прогрессия виды:

a+ a*q+a*q²+…+a*q^n-1+… = , a≠0