Признак Лейбница

Если члены знакочередующегося ряда 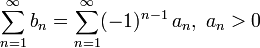убывают по абсолютной величине 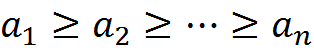и 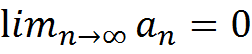, то ряд сходится, а его сумма S положительна и не превосходит первого члена: S<=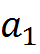

Пример 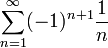. Ряд из модулей имеет вид 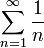— это гармонический ряд, который расходится.

Теперь воспользуемся признаком Лейбница:

знакочередование выполнено , ,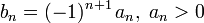

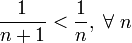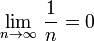
Следовательно, так как все условия выполнены, но ряд из модулей расходится, искомый ряд сходится условнo