Фактор-пространство ТП по данному разбиению(1). Естественное отображение ТП на его фактор-пространство и его свойства(2)

(1) Пусть D –разбиение пр-ва Х. Пр-во называется фактор-пространством пр-ва по разбиению D и обозначается X/D.

(2) Отображение q:X 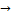X/D, которое каждой точке ставит в соответствие тот единственный элемент разбиения D, который содержит точку 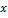, называется естественным отображением пространства Х на фактор-пространство X/D.

q-cюрьективно, кроме того, 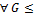X/D справедливо утв:

G открыто в X/D <=> открыто в X. Отсюда так же следует что q непрерывно.

Следовательно, Если Х комп, св. или лин.св., то таким же свойством обладает и любой его фактор.

46.Понятие факторного отображения топологических пространств. Достаточные условия, при выполнении которых сюръективное непрерывное отображение является факторным.

Опр

Пусть X,Y–Т.П. Сюръект отображение f:X—>Y называется факторным если для любого Uc_Y выполн условие:

Uc__op Yó f^-1 (U)c__opX

Замечание

1) Любое факторное отображение непрерывно

2) Естественное отображение пр-ва Х на любое его фактор-пр-во является факторным

Утв Пусть X,Y–Т.П. f:X—>Y - непрерывно, сюръект отображение. Если для f выполняется хотя бы одно из условий

1) для любого U c__opX, f (U)c__{op Y}

2) для любого F c__cl X, f(F)c__cl Y; то f является факторным отображением

▫ 2) Пусть Uc__op Y => f^-1 (U)c__opX т.к f- непрерывно. Пусть Uc_Y и f^-1 (U)c__opX => Uc__op Y. Пусть F=Y\U; f^-1 (F)=X\ f^-1 (U) т.к f^-1 (U)c__opX => f^-1 (F)c__cl X f(f^-1 (F))=F => F c__cl Y=> Uc__op Y ▪

Следстви е Пусть X,Y - Т.П. f:X—>Y - непрерывн сюръект отображение. Если X - компактно, Y - хаусдорфово, то f - факторное отображение

▫ Пусть F c__cl X => F – компакт => f(F) – компакт, т.к. Y - хаусдорфово f(F)c__clY ▪

47. теорема о связи между конструкцией фактор-пространства и факторными отображениями. Пример фактор-пространства.

Утв Пусть X,Y - Т.П. f:X—>Y - факторное отображение. Рассм разбиение D(f)={f^-1 (y)ǀyϵY} пр-ва X. Ǝ гомеоморфизм h:X/D(f) —>Y,удовлетвор условию: для любого xϵX f(x)=h(g(x)), где g:X—> X/D(f) естеств отображение

▫ Рассм отоб-е h:X/D(f) —>Y определен по правилу f-¹ (y) —^h >y. Тогда:h-биекция и для любогоxϵX f(x)=h(g(x)) Непрерывность h: Пусть Uc__op Y; f^-1 (U) c__op X, f^-1 (U)=g^-1 (h^-1 (U)) => h^-1 (U) c__op X/D(f). Покажем, что h^-1 :Y —> X/D(f) - непрерывно. Пусть Gc__op X/D(f). Покажем, что (h^-1)^-1(G)c__op Y, т.е. h(G) c__op Y. Покажем, что f^-1(h(G))= g^-1 (h^-1(h (G)))= g^-1(G) c__op X => h(G)c__op Y ▪

Примеры

1) Рассм отрезок I=[0,1] c_R. Разбиение D состоит из{0,1} и всех эл-в вида {t} где tϵ ]0,1[ Рассм на R² подпр-во S¹ :x² +y² =1 и покажем, что I/D ≈s¹ . Рассм f:I —> s¹, f(t)=(cos 2πt, sin2πt) f - факторное отображение I/D≈ S¹

2) На пл-ти R² рассм квадрат K:

Разбиение D сост. из всех мно-тв вида: {(0,v),(1,v)}, 0≤v≤1 и всех м-тв вида {(u,v)}, o<u<1, 0≤v≤1

Покажем что K/D гомеоморф фигуре C в R³ зададен системой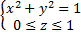

Рассм f:K —>C f(u,v)=(cos2πu, sin2πu, v) D(f)=D, f – факторное => K/D≈C

№1. Понятие метрического пр-ва. Примеры. Шары и сферы. Ограниченные и неограниченные мн-ва в метрическом пр-ве. Диаметр мн-ва. Изометрия и изометрическое вложение.

№2. Топология метрического пр-ва. Открытый шар как открытое мн-во. Св-ва открытых мн-в.

№3. Подпространство метрического пр-ва и его топология.

4. Топологические пространства. Окрестности. Метризуемые и неметризуемые пространства. Примеры метризуемого и неметризуемого пространств. Естественная топология на R^n. Понятие топологической эквивалентности метрик. Пример топологически эквивалентных метрик на R^n.

5. Замкнутые множества в топологическом пространстве и их свойства.

6. Подпространства топологического пространства. Индуцированная топология. Замкнутые множества в подпространстве. Примеры: Z как подпространство R. Пример открыто-замкнутого множества в подпространстве Q прямой R.

7. Хаусдорфовы пр-ва.

8.Предел последовательности.

9.Замыкание мн-ва

№10. Внутренность множества в топологическом пространстве и её св-ва (в том числе характеристика открытых множеств, через понятие внутренности)

№11. Граница множества в топологическом пространстве и её св-ва (в том числе формула связывающая замыкание, внутренность и границу множества)

№12. База топологического пр-ва. Утверждение, характеризующее базы. Локальная база пр-ва в данной точке. Первая и вторая аксиомы счётности и связь между ними. Первая аксиома счётности и метризуемость. Аксиомы счётности и подпространства.

13.Всюду плотные множества в топологических пространствах. Сепарабельность. Связь между сепарабельностью и второй аксиомой счетности. Пример: существование счетной базы в

14. Сравнение топологий.

15. Сравнение метрических топологий. Критерий топологической эквивалентности метрик

16. Непрерывное отображение топологических множеств. Определения. Примеры. Теорема о непрерывности композиции

17. Критерий непрерывности отображений топологических пространств.

18. Сужение отображение на подпространство топологического пространства и его непрерывность (2 теоремы)

19.Операции над вещественно-значимыми непрерывными функциями

20.Секвенциально непрерывные отображения топологических пространств.

Связь между непрерывностью и секвенциальной непрерывностью

21.Понятие гомеоморфизма. Пример: стереографическая проекция. Пример непрерывной биекции, не являющейся гомеоморфизмом

22.Метод введения топологии с помощью базы.

23 Определение топологии произведения топологических пространств. Теорема о метричности этой топологии. Примеры.

24 Сходимость последовательностей в произведении топологических пространств.

25. Проектирование на произведении топологических пространств и их непрерывность отображения в произведении.

26. Связные пространства, Простейшие хар-ки несвязан. Примеры: связность отрезка и несвязность ℚ(как подпростр. ℝ)

27.Сохранение связности непрерывными отображениями. Теорема о промежуточных значениях.

28.Сохранение связности непрерывных отображений. Теорема о промежуточных значениях

29 Линейно связные пространства. Связь между связностью и линейной связностью. Сохранение линейной связности непрерывными отображениями. Примеры линейно связных пространств.

30.Связность замыкания связного множества. Свойства веера.

31) Связные компоненты топологического пространства и их свойства. Пример: связные компоненты Q (как подпространства R)

32) Понятие компактного топологического пространства. Характеристика компактности через центрированные семейства замкнутых множеств. Примеры.

33) Теорема о компактности произведения компактных пространств

34 Компактность замкнутого подпространства компактного пространства.

Замкнутость компактных множеств в хаусдорфовом пространстве. Нормальность компактных хаусдорфовых пространств. Критерий компактности в Rⁿ

35 Сохранение компактности непрерывными отображениями. Теорема Вейерштрасса. Пример ограниченного непрерывного отображения из R в R, не имеющего ни точки максимума, ни точки минимума

36 Теорема о непрерывной биекции компактного пространства на хаусдорфово. Пример: граница выпуклого многоугольника на плоскости R² гомеоморфна окружности

37.Полные метрические пространства. Примеры полных и неполных пространств. Полнота. Полнота подпространств.

38. Убывающие последовательности замкнутых множеств в полных метрических пространствах.

39.Вполне ограниченные метрические пространства. Связь между ограниченностью и вполне ограниченностью. Вполне ограниченные множества в (Rⁿ, d) (d-евклидова метрика)

40 Критерий того, что метрическое пространство не является вполне ограниченным. Пример: замкнутый шар в пространстве С[0,1] с метрикой равномерной сходимости как ограниченное, но не вполне ограниченное множество

41 Теорема о связи между компактностью, полнотой и полной ограниченностью метрических пространств: доказательство того, что компактное метрическое пространство является полным и вполне ограниченным

42 Теорема о связи между компактностью, полнотой и полной ограниченностью метрических пространств: доказательство того, что полное и вполне ограниченное метрическое пространство компактно.

43. Критерий компактности полного метрического пространства.

44. Предельные точки множеств в ТП. Критерий компактности метризуемого ТП(последовательности и предельности).

45. Фактор-пространство ТП по данному разбиению(1). Естественное отображение ТП на его фактор-пространство и его свойства(2).

46.Понятие факторного отображения топологических пространств. Достаточные условия, при выполнении которых сюръективное непрерывное отображение является факторным.

47. теорема о связи между конструкцией фактор-пространства и факторными отображениями. Пример фактор-пространства.

Определения

Пусть X непустое мн-во, элементы которого будем наз. точками. Метрикой на X наз. Отображение удовл. аксиомам:

М1)

M2)

M3)

Пара (X, ρ) называется метрическим пространством

Пусть -топологическое пр-во. называется ограниченным если .

Диаметром ограниченного мн-ва А называется число . Если A не ограниченное то

Пусть и метрические пр-ва. Отображение 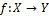называется изометрией, если

f -биекция

. Если существует изометрия 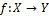, то метрики пр-ва X и Y называется изометричными.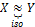

Пусть -метрическое пр-во. называется открытым, если Пустое мн-во по определению считаем открытым. Совокупность всех открытых мн-в метрического пр-ва называется топологией этого пр-ва и обозначается 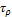. -открытое подмн-во пр-ва

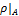Пусть -топологическое пр-во. . Обозначим через - сужение на Метрическое пр-во - называется подпространством метрического пространства . Метрика 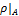- называется индуцированной метрикой.

Опр. Пусть Х множество, элементы которого будем называть точками. Топологией на Х называется семейство τ подмножеств множества Х, удовлетворяющее аксиомам:

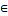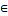1.Ø τ, ч τ

2.Пересечение любой конечной совокупности множеств из τ, принадлежит τ.

3.Объединение любой совокупности множеств из τ принадлежит τ.

Опр. Пара (Х, τ) называется топологическим пространством, а множество семейства τ – открытыми множествами пространства (Х, τ).

Опр. Окрестностью точки х 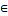Х называется любое открытое множество содержащее эту точку.

Опр. Окрестностью множества А 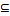Х называется любое открытое множество содержащее А.

U 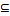(под символом 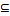указать ор) Х – U открытое подмножество пространства Х.

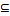Опр. Пусть Х- топологическое пространство; Множество F Х называется замкнутым, если его дополнение Х\F открыто. F Х(под знаком указать cl)-F является замкнутым множеством пространства Х.

Опр. Пусть (Х, τ) топологическое пространство, А 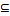Х – подмножество из Х. Семейство

τ/_А={ u A| u 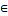τ} является топологией на А. Топологической пространство (А, τ/_А ) над подпространством пространства (Х, τ), а топология τ/_А индуцированной топологией.

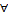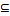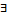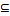Таким образом u A выполняется: U А(под знаком указать op). Ũ (под знаком указать op) Х | Ũ(u с волной) A=u.

Т. П. Х наз. хаусдорфовым если у любых двух различных точек этого пространства существуют непересекающиеся окрестности.

Последовательностью точек Т.П. (Х, τ) наз отображение N→X, n--> . Запись

Пусть -топологическое пр-во. Семейство называется базой пр-ва X, если любое непустое открытое множество можно представить в виде объединения некоторого подсемейства семейства P.

Пусть (Х,τ₁) и (Y,τ₂) – Т.П. Отображение F: Х—>Y называют непрерывным в т. х ϵ Х, если для любой окрестности U точки f(x) Ǝ окрестность V точки х ǀ f(V)c_ U. Отображение называется непрерывным, если оно непрерывно в каждой точке. Множество всех отображений из X в Y обозначатся C(X,Y). Если Y=R, то С(Х).

Опр. Пусть X, Y – Т.П. Отображение f: X → Y Называется гомеоморфизмом, если:

1) f-биекция

2) f-непр.

3) f^-1: Y→X-непр

Если Ǝ гомеоморфизм f: X → Y то пр-ва X и Y называются гомеоморфными (X≈Y)
Пусть даны т.п. , x= 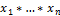Топологией произведения на Х наз. топология _r базу которой образует сем-во β_n

ТП. Х наз. несвязным если его можно представить в виде двух непустых непересекающихся открытых мн-в(т.е. в виде X где U . Х наз. связным если оно не явл. несвязным.

Пусть Х- Т.П. Семейство α подмножеств пространства Х называется покрытием пространства Х, если α=Х. Если α – покрытие пространства Х называется подпокрытием покрытия α.

Покрытие называется открытым, если его элементы – открытые множества.

Т.П. Х называется компактным, если любое его открытое покрытие содержит конечное подпокрытие.

Множество А называется компактным, если оно компактно как подпространство с индуцированной топологией

Пусть X,Y–Т.П. Сюръект отображение f:X—>Y называется факторным если для любого Uc_Y выполн условие:

Uc__op Yó f^-1 (U)c__opX