 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Компактность замкнутого подпространства компактного пространства
|
|
Замкнутость компактных множеств в хаусдорфовом пространстве. Нормальность компактных хаусдорфовых пространств. Критерий компактности в Rn
1 Любое замкнутое подпространство компактного пространства компактно.
□ Пусть F  X, X копмактно. Покажем, что F – комактно.
X, X копмактно. Покажем, что F – комактно.
Пусть ξ- центрированное семейство замкнутых множеств подпространства F. Так как F замкнуто, то ξ- центрированное семейство замкнутых множеств в пространстве Х. Следовательно,  ξ
ξ  Ø ■
Ø ■
2 Любое компактное пространство хаусдорфова пространства замкнуто.
□ Пусть β –компактное подпространство хаусдорфова пространства Х.
Рассмотрим для  точки b
точки b 
 окрестность Ub(х) точки х и окрестность V(b) точки b такие, что Ub(х)
окрестность Ub(х) точки х и окрестность V(b) точки b такие, что Ub(х)  V(b)= Ø. Так как В – компактно, то
V(b)= Ø. Так как В – компактно, то  b1..bn такие, что В
b1..bn такие, что В  V(b1)
V(b1)  ..
..  V(bn). Пусть U=Ub1(x)
V(bn). Пусть U=Ub1(x)  ..
..  Ubn(x), V=V(b1)
Ubn(x), V=V(b1)  ..
..  V(bn). U
V(bn). U  V= Ø, U
V= Ø, U  B = Ø ■
B = Ø ■
Компактное хаусдорфово пространство нормально(т.е. у любых двух непересекающихся множеств компактного хаусдорфового пространства существуют непересекающиеся окрестности)
Критерий компактности в Rn: Подпространство А  Rn компактно
Rn компактно  А замкнуто и ограничено
А замкнуто и ограничено
□  ) В силу (2) А – замкнуто. Рассмотрим семейство
) В силу (2) А – замкнуто. Рассмотрим семейство  .
.  - покрытие для А. Так как А – компактно,
- покрытие для А. Так как А – компактно,  - как покрытие А содержит конечное подпокрытие Bn(o,k1).. Bn(o,kn). Пусть Bn(o,ki) – наибольший шар, тогда
- как покрытие А содержит конечное подпокрытие Bn(o,k1).. Bn(o,kn). Пусть Bn(o,ki) – наибольший шар, тогда  А – ограничено.
А – ограничено.
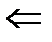 ) Так как А ограничено
) Так как А ограничено  параллелепипед П
параллелепипед П  А. А замкнуто в Rn
А. А замкнуто в Rn  . П – компактно
. П – компактно  А компактно ■
А компактно ■
35 Сохранение компактности непрерывными отображениями. Теорема Вейерштрасса. Пример ограниченного непрерывного отображения из R в R, не имеющего ни точки максимума, ни точки минимума
Непрерывный образ компактного пространства компактен (если f: X → Y непрерывно и сюръективно и Х – компактно, то Y – компактно).
□ Рассмотрим  открытое покрытие
открытое покрытие  пространства Y. Рассмотрим
пространства Y. Рассмотрим  - открытое подпространство Х. Так как Х – компактно,
- открытое подпространство Х. Так как Х – компактно,  содержит конечное подпокрытие, то есть
содержит конечное подпокрытие, то есть 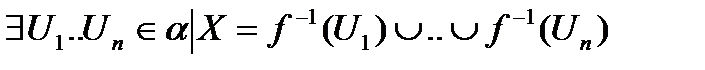
 ■
■
Непрерывная функция f: X → R, определенная на компактном топологическом пространстве Х, ограничена. Кроме того существуют точки, где f принимает как максимальные, так и минимальные значения.
□ Так как Х – компактно, f(x) компактно в R  f(x) замкнуто и ограничено. f(x) ограничено
f(x) замкнуто и ограничено. f(x) ограничено  f ограничено. Пусть a = inf f(x), b = sup f(x). Так как f(x) замкнуто, a, b
f ограничено. Пусть a = inf f(x), b = sup f(x). Так как f(x) замкнуто, a, b  f(x)
f(x) 
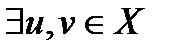 . f(u) = a, f(v) = b
. f(u) = a, f(v) = b  f(u)
f(u)  f(x)
f(x)  f(v) ■
f(v) ■
Рассмотрим f: R→ R (R – не компактно).
f(x) = arctg x.

36 Теорема о непрерывной биекции компактного пространства на хаусдорфово. Пример: граница выпуклого многоугольника на плоскости R2 гомеоморфна окружности
Непрерывная биекция компактного пространства на хаусдорфово является гомеоморфизмом
□ X,Y - топологические пространства. Х – компактно, Y - хаусдорфово. Требуется доказать, что f является гомеоморфизмом. Покажем, что f-1: Y →X непрерывно. Покажем, что 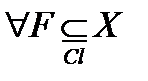


 F – компакт
F – компакт  f(F) компакт. Y хаусдорфово
f(F) компакт. Y хаусдорфово 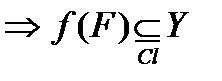 ■
■

Дата публикования: 2015-11-01; Прочитано: 1057 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
