Понятие компактного топологического пространства. Характеристика компактности через центрированные семейства замкнутых множеств. Примеры

Опр.1 Пусть Х- Т.П. Семейство α подмножеств пространства Х называется покрытием пространства Х, если α=Х. Если α – покрытие пространства Х называется подпокрытием покрытия α.

Покрытие называется открытым, если его элементы – открытые множества.

Опр.2 Т.П. Х называется компактным, если любое его открытое покрытие содержит конечное подпокрытие.

Множество А называется компактным, если оно компактно как подпространство с индуцированной топологией

Замечание. Подмножество А, Т.П. Х компактно любое семейство α открытых в Х множеств такое, что А α содержит конечное подсемейство (в этом случае α также будет называть покрытием А, подпокрытие покрытия α. ) Пусть α семейство открытых в Х множеств, А α, рассмотрим }, тогда 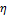– покр. А множествами, открытыт. в А. содержит конечно подпокрытие, т.е. 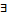U₁ … U_n | (U₁ А) … (U_n А) =А А 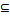U₁ … U_n

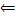) Рассм. – покрытия А множествами, открытых в А. V |

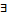
Рассмотрим α={ }; A α. По условию 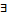U₁ … U_n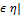 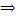V₁... V_n=A

Пример. 1) 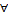n пространство Rⁿ не компактно. α={ Bⁿ (0,k) | k }

k

-k … -2 -1 1 2 … k

n=1

n=2

α открытое пространство Rⁿ не содержащее

конечного покрытия

Опр.3 Семейство подмножеств ТП Х называется центрированным

если пересечение любого конечного подсемейства семейства не пустое.

Пример. в R 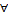n F_n= [n, F_n| n – центрировано

nk

n2

n1

Утв. ТП Х компактно пересечение любого центрального семейства замкнутых множеств в Х не пусто.

) от противного. Допустим 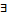центральное семейство замкнутых множеств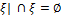

Рассмотрим α={X \ F | F 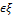} Таким образом α – открытое покрытие пространства Х.

Х компактно содержит конечное подпокрытие, т.е.. 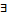F₁ … F_n 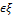| (x \ F₁ … x \ F_n)=X

Тогда F₁ … F_n= ?!

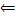) от противного. Допустим 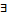открытое покрытие не содержащее конечное подпокрытие.

{X \ U | U } Пусть F₁ … F_n 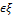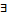U₁ … U_n | X \ U₁ = F₁, … X \ U_n = F_n

F₁ … F_n = (X \ U₁ … (X \ U_n)=X \ (U₁ … U_n) Но ?!