Предельные точки множеств в ТП. Критерий компактности метризуемого ТП( последовательности и предельности)

Опр. Пусть Х- ТП., А содержится в X. Точка называется предельной для А, если 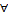окрестность U точки : - бесконечно.

Критерий. Пусть Х – метризуемое ТП. Следующие условия эквиваленты:

(а) Х- компактно.

(б) Любое бесконечное множество А содержащееся в Х имеет в Х предельную точку.

(в) Любая последовательность точек пр-ва Х содержит сходящуюся подпоследовательность.

!(а)=>(б)! от против.

Допустим бесконечное мн-во А содержащееся в X не имеющее предельной точки. Тогда - конечно.

Семейство – открытое покрытие Х. Х-компактно =>

А содержится в X=> A содержится в , как?!

!(б)=>(в)! Рассмотрим послед . Пусть . Если М конечно, то послед содержит подпослед вида . Она является сходящейся.

Пусть М бесконечно, тогда существует предел точки мн-ва М. Покажем тто содержит подпослед сходящуюся к . Построим последовательность которая удлвлетворяет условиям при :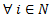

1)

2)

Если определено, то Подпослед последовательности сходится к , т.к.

!(в)=>(а)! Пусть - метрика, соглас. с топологией Х. Покажем, что полная и вполне огр.

Полнота. Пусть - фундаментальная послед. По усл. содержит сходящуюся подпоследлвательность. По Лемме 2 послед сходится.

Вполне огр. (от против.) Допустим не вполне огр. По определению и послед | . Послед не содержит сходящихся подпослед. ?!