Приклад розрахунку. 1. Знайти наближення функції на інтервалі [0. 0; 1. 2] з використанням лінійного p1(x), квадратичного p2(x) та кубічного p3(x) поліномів Лаґранжа

1. Знайти наближення функції на інтервалі [0.0; 1.2] з використанням лінійного P ₁(x), квадратичного P ₂(x) та кубічного P ₃(x) поліномів Лаґранжа.

Розв’язок

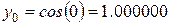Побудуємо лінійний поліном P ₁(x) за точками і , використовуючи (4.3) з абсцисами і та ординатами і :

Побудуємо інші поліноми Лаґранжа: квадратичний P ₂(x) за трьома вузлами , і ; кубічний поліном P ₃ (x) за чотирма – , , і .

Виконаємо підстановку , , і 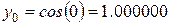, , у формулу (4.8):

Підставивши , , і і 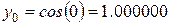, , , до (4.9), отримаємо:

2. Для значень x, що розбивають інтервал [0.0; 1.2] з кроком 0.1, розрахувати значення функції , значення поліномів Лаґранжа P ₁ (x), P ₂ (x), P ₃ (x) та зобразити розв’язок у табличному й графічному вигляді. Визначити помилки наближень. Порівняти результати наближення з точним розв’язком та проаналізувати точність поліномів Лаґранжа між собою.

Розв’язок

Значення помилок наближень Лаґранжа E ₁(x), E ₂(x), E ₃(x) для поліномів P ₁(x), P ₂(x), P ₃(x) відповідно наведені в табл. 4.5.

Таблиця 4.5 – Порівняння значень функції f (x) з лінійним, квадратичним і кубічним наближеннями Лаґранжа P ₁(x), P ₂(x), P ₃(x)

xk	f (xk)=cos (xk)	E 1(xk) = f (xk) -P 1(xk)	E 2(xk) = f (xk) -P 2(xk) )	E 3(xk) = f (xk) -P 3(xk)
0.0	1. 000000	0. 000000	0. 000000	0. 000000
0.1	0. 995004	0. 048141	0. 004093	-0. 000831
0.2	0. 980067	0. 086340	0. 006253	-0. 000855
0.3	0. 955336	0. 114747	0. 006629	-0. 000476
0.4	0. 921061	0. 133608	0. 005469	0. 000000

Продовження таблиці 4.5

0.5	0. 877583	0. 143267	0. 003114	0. 000361
0.6	0. 825336	0. 144157	0. 000000	0. 000890
0.7	0. 764842	0. 136800	-0. 003352	0. 000351
0.8	0. 696707	0. 121802	-0. 006338	0. 000000
0.9	0. 621610	0. 099842	-0. 008276	-0. 000438
1.0	0. 540302	0. 071671	-0. 008416	-0. 000765
1.1	0. 453596	0. 038102	-0. 005946	-0. 000724
1.2	0. 362358	0. 000000	0. 000000	0. 000000

У табл. 4.6 наведено оцінки середньоквадратичних відхилень помилок наближень поліномами Лаґранжа P ₁(x), P ₂(x), P ₃(x), що розраховуються за формулою:

, (4.23)

де – значення вибірки з N елементів;

– математичне очікування чи середнє арифметичне вибірки.

Таблиця 4.6 – Оцінки середньоквадратичних відхилень помилок наближень поліномами Лагранжа.

Поліном	P 1(x), k= 1	P 2(x), k= 2	P 3(x), k= 3
	0.054357	0.005736	0.000566

Наближення поліномом P ₃(x) до має найкращу точність, оскільки має найменше значення середньоквадратичного відхилення помилки. З табл. 4.6 бачимо, що зі збільшенням степеня інтерполяційного полінома підвищується точність наближення до функції .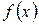

Графіки наближення функції лінійним P ₁(x), квадратичним P ₂(x) і кубічним P ₃(x) поліномами Лаґранжа наведено на рис. 4.1, де чорними точками позначено вузли інтерполяції.

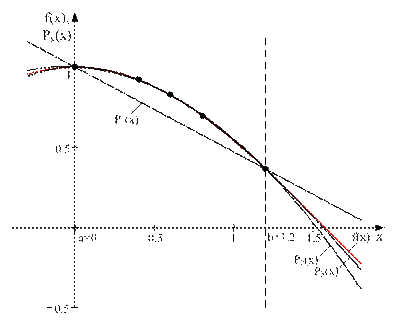
Рисунок 4.1 – Графіки наближення функції лінійним P ₁(x), квадратичним P ₂(x) і кубічним P ₃(x) поліномами Лаґранжа на інтервалі [0.0; 1.2]

Графіки помилок наближень , , відповідно лінійним P ₁ (x), квадратичним P ₂ (x) і кубічним P ₃ (x) поліномами Лаґранжа зображено на рис. 4.2, де чорними точками позначено вузли інтерполяції.

Рисунок 4.2 – Графіки помилок наближень функції лінійним P ₁ (x), квадратичним P ₂ (x) і кубічним P ₃ (x) поліномами Лаґранжа на

інтервалі [0.0; 1.2]

3. Побудувати таблицю різницевих відношень для функції за точками x_k, для та знайти поліноми Ньютона P ₁(x), P ₂(x), P ₃(x), P ₄(x).

Розв’язок

Наступна модель обчислень показує, як знайти коефіцієнт a ₂ через різницеві відношення:

Значення різницевих відношень наведені в табл. 4.7.

Таблиця 4.7 – Таблиця різницевих відношень для функції

	1. 0000000
	0. 5403023	-0. 4596977
	-0. 4161468	-0. 9564491	-0. 2483757
	-0. 9899925	-0. 5738457	0. 1913017	0. 1465592
	-0. 6536436	0. 3363499	0. 4550973	0. 0879318	-0. 0146568

Використаємо табл. 4.7, щоб знайти коефіцієнти a_k і чотири інтерполяційні поліноми Ньютона P_k (x) для k =1, 2, 3, 4.

Запишемо поліноми Ньютона з використанням формули (4.18) за вузлами та елементами (коефіцієнтам поліномів Ньютона), які знаходяться на діагоналі табл. 4.7:

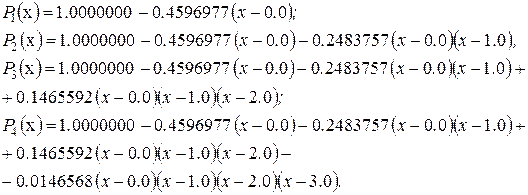
4. Для значень x, що розбивають інтервал [0; 1.2] з кроком h, розрахувати значення функції , поліномів Ньютона P ₁(x), P ₂(x), P ₃(x), P ₄(x) та подати розв’язок у табличному й графічному вигляді з використанням пакетів Mathcad та Matlab. Порівняти результати наближення з точним розв’язком та проаналізувати точність поліномів Ньютона між собою

Розв’язок

Значення помилок наближень E ₁(x), E ₂(x), E ₃(x), E ₄(x) для поліномів Ньютона P ₁(x), P ₂(x), P ₃(x), P ₄(x) відповідно наведено в табл. 4.8.

Таблиця 4.8 – Порівняння f (x) з наближеннями Ньютона P ₁(x), P ₂(x), P ₃(x), P ₄(x)

xk	f (xk)	E 1(x k)	E 2(xk)	E 3(xk)	E 4(xk)
0.0	1. 000000	0.000000	0.000000	0.000000	0.000000
0.1	0. 995004	0.040974	0.018620	-0.006442	-0.01371
0.2	0. 980067	0.072006	0.032266	-0.009943	-0.021762
0.3	0. 955336	0.093246	0.045330	-0.011235	-0.025362
0.4	0. 921061	0.104940	0.041544	-0.010949	-0.025582
0.5	0. 877583	0.107431	0.041087	-0.009622	-0.023363
0.6	0. 825336	0.101154	0.045337	-0.007700	-0.019519
0.7	0. 764842	0.086631	0.034472	-0.005539	-0.014742
0.8	0. 696707	0.064465	0.024725	-0.003415	-0.009606
0.9	0. 621610	0.035338	0.012984	-0.001525	-0.004572
1.0	0. 540302	0.000000	0.000000	0.000000	0.000000
1.1	0. 453596	-0.040736	-0.013415	0.001094	0.003851
1.2	0. 362358	-0.086005	-0.026395	0.001744	0.006810

У табл. 4.9 наведено оцінки середньоквадратичних відхилень помилок наближень поліномами Ньютона P ₁(x), P ₂(x), P ₃(x), P ₄(x).

Таблиця 4.9 – Оцінки середньоквадратичних відхилень помилок наближень поліномами Ньютона

Поліном	P 1(x), k= 1	P 2(x), k= 2	P 3(x), k= 3	P 4(x), k= 4
	0.063592	0.024668	0.005016	0.012071

Аналіз табл. 4.9 свідчить, що поліном Ньютона з найвищим степенем P ₄(x) не є найкращим наближенням функції . Для наближення на відрізку [0.0; 1.2], краще використовувати поліном P ₃(x), оскільки він має найменше значення оцінки середньоквадратичного відхилення помилки наближення.

Графіки наближення функції поліномами Ньютона різного степеня P ₁(x), P ₂(x), P ₃(x), P ₄(x)наведено на рис. 4.3, де чорними точками позначено вузли інтерполяції.

Рисунок 4.3 – Графіки наближення функції поліномами Ньютона різного степеня на інтервалі [0.0; 1.2]

Графіки помилок наближень , , , відповідними поліномами Ньютона P ₁(x), P ₂(x), P ₃(x), P ₄(x) зображено на рис. 4.4, де чорними точками позначені вузли інтерполяції.

Рисунок 4.4 – Графіки помилок наближень функції поліномами Ньютона різного степеня на інтервалі [0.0; 1.2]

З табл. 4.6 і 4.9 видно, що поліноми Лаґранжа порівняно з поліномами Ньютона того ж степеня дають меншу помилку наближення до функції на інтервалі [0.0; 1.2]. У зв’язку з цим, при розв’язанні різних задач для інтерполяції функції на інтервалі [0.0; 1.2] краще використовувати поліноми Лаґранжа.

5. Знайти наближення Паде R _4,4(x) для функції . Подати розв’язок у графічному вигляді з використанням пакетів Mathcad чи Matlab. Визначити помилку наближення.

Розв’язок

Виконаємо розклад функції у ряд Маклорена:

З урахуванням розкладання Маклорена рівняння (4.20) набуває вигляду:

Виконавши перетворення та дорівнявши коефіцієнти при перших дев’яти степенях x у лівій і правій частинах, отримаємо дві системи з дев’яти лінійних рівнянь:

; .

Розв’язок спочатку другої, а потім першої з отриманих систем лінійних рівнянь дозволяє знайти значення невідомих коефіцієнтів наближення Паде: .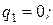

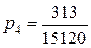Тоді раціональне наближення Паде R _4,4(x) для функції :

На рис. 4.5 зображено графіки функції і її наближення за допомогою рядів Паде R _4,4(x). Графік помилки Е_R (x) наближення Паде R _4,4(x) зображено на рис. 4.6.

Рисунок 4.5 – Наближення Паде R _4,4(x) для функції

Рисунок 4.6 – Графік помилки наближення Паде R _4,4(x) для функції

ЗАВДАННЯ №5